Resolver las ecuaciones diferenciales ejercicios
Clasifique las ecuaciones diferenciales según sus propiedades
1 Respuesta
Respuesta de Lucas m
1
;)
Hola Elen!
Pon las preguntas siempre en matemáticas, además de otros temas (Calculo, Profesores, Ingeniería) sino puede que no las vea
Las ecuaciones diferenciales se clasifican por tipo, orden y linealidad
Si una ecuación contiene derivadas ordinarias de una o más variables dependientes con respecto a una sola variable independiente se dice que es una ecuación diferencial ordinaria (EDO)
Si una ecuación con derivadas de una o más variables dependientes de dos o más variables independientes se llama ecuación diferencial parcial (EDP)
a) EDO
b)EDO
El orden de una ecuación diferencial (ya sea EDO o EDP) es el orden de la derivada mayor en la ecuación
a) Orden 4
b) Orden 3
Se dice que una ecuación diferencial ordinaria de orden n es lineal si F es lineal en y, y',..., y(n). Esto significa que una ecuación diferencial ordinaria de orden n es lineal cuando F (x, y, y',..., y(n)) = 0 es:
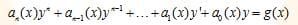
En la combinación aditiva en el lado izquierdo de la anterior podemos afirmar que:
La variable dependiente "y" y todas sus derivadas y', y'',..., y(n) son de primer grado. Y los coeficientes a0, a1,..., an dependen solo de la variable x.
Los ejemplos de ecuaciones diferenciales lineales se tiene las siguientes:
a) y''+xy'-3y=e^2x ,
b) y''' + y'' + y = 0,
c) (1-x) y'' - 4xy' + 5y = cos x
Los ejemplos de ecuaciones no lineales tenemos:
a) (1-y) y'' - 2y= e^x, es una ecuación diferencial no lineal porque el coeficiente de la variable dependiente y'' también depende de y.
b) y'' + sen y = 0 Es una ecuación diferencial no lineal porque la función seno es función de y
c) y'' + y^2 = 0, es una ecuación diferencial no lineal porque la potencia de la variable y es 2, y no 1 para que sea lineal.
d) (y''')^3 + xy'' - 3y = 0, es una ecuación diferencial no lineal porque la potencia de la variable y''' es 3 y para ser lineal debe ser 1
En tu caso:
a) Es Lineal
b) No es Lineal, ya que el segundo término tiene una derivada segunda elevada a la quinta
A parte de esto, las dos son No Homogéneas
Una ecuación diferencial de orden superior que tiene la forma:
.
Saludos
;)
;)
