Problema de calculo integral, como puedo resolver este ejercicio

;)
Hola recce pacheco!
Eso es una Suma de Riemann por el punto medio, donde vamos a aproximar el área bajo la curva a partir de n=4 rectángulos de bases iguales y alturas la imagen del punto medio de cada intervalo.

Es decir:

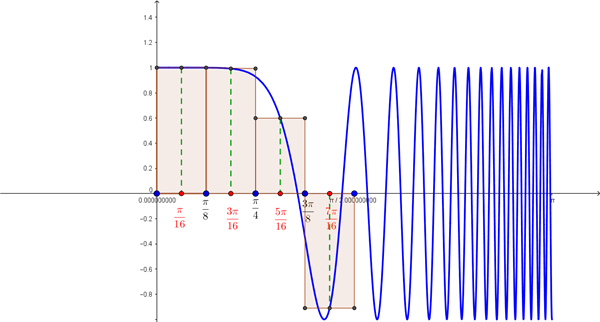
$$\begin{align}&\int_a^b f(x) dx= \sum _{i=1}^n f(\overline{x_i}) \Delta x\\&\\&base \ de \ los \ rectángulos: \\&\Delta x= \frac{b-a} n=\frac{ \frac \pi 2 -0} 4= \frac \pi 8\\&intervalos:\\&[0, \frac{\pi} 8] ==> punto\ medio\ \ \overline{x_1}= \frac{\pi}{16}\\&\\&[ \frac{\pi} 8 ,\frac {2 \pi} 8]==>\overline {x_2}= \frac{ \frac{\pi} 8 + \frac{ 2 \pi} 8} 2= \frac{3 \pi }{16}\\&\\&[ \frac{2pi} 8 ,\frac {3 \pi} 8]==>\overline {x_3}= \frac{ \frac{2 \pi} 8 + \frac{ 3 \pi} 8} 2= \frac{5 \pi }{16}\\&\\&[ \frac{3 \pi} 8 ,\frac {4 \pi} 8]==>\overline {x_2}= \frac{ \frac{3  \pi} 8 + \frac{ 4 \pi} 8} 2= \frac{7 \pi }{16}\\&\\&\int_0^{2 \pi} f(x) dx \simeq \sum _{i=1}^n f(\overline{x_i}) \Delta x= \Delta x \Bigg( f(\overline {x_1})+f(\overline {x_2})+f(\overline {x_3})+f(\overline {x_4 }) \Bigg)=\\&\\&= \frac{\pi} 8 \Bigg(\cos(\frac {\pi}{16})^4 +\cos(\frac {3 \pi}{16})^4+\cos(\frac {5 \pi}{16})^4+\cos(\frac {7 \pi}{16})^4 \Bigg)\\&\\&=1.3765\end{align}$$

Recuerda que la calculadora hade estar en  MODE Radian

Saludos

;)

;)