Encontrar el área comprendida entre las curvas

;)
Hola Sophia!

Para calcular el área comprendida entre dos funciones f(x) i g(x) se plantea la integral:

$$\begin{align}&\int_a^b(f-g)dx\end{align}$$

donde x=a y x=b  son las rectas verticales que limitan el recinto

F la función que está por arriba

G la función que está por abajo.

Si no te dan el esquema, no pasa nada, haces la integral de la diferencia de una función menos la otra, y se toma el valor absoluto del resultado (si te da negativo, es pq las has colocado al revés)

También hay que calcular los puntos de corte de las dos funciones: si hay dos==> un recinto

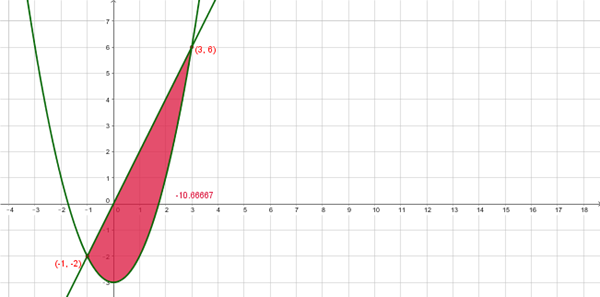
$$\begin{align}&y=2x\\&y=x^2-3\\&\\&Puntos de corte==>Igualando\\&x^2-3=2x\\&\\&x^2-2x-3=0\\&\\&x_1=-1\\&x_2=3\\&\\&Area=\int_{-1}^3 2x-(x^2-3)]dx=\Big[x^2- \frac{x^3} 3+3x \Big]_{-1}^3=\\&\\&\Big(3^2- \frac {3^3} 3+3(3) \Big)-\Big((-1)^2- \frac{(-1)^3} 3+3(-1)\Big)=\\&9-9+9-(1+ \frac 1 3-3)= \frac { 32}  3\ =10. \overline 6 \ \ u^2\end{align}$$

Te recuerdo que si tienes una calculadora científica (Casio 991 o similar) tienes una tecla para  calcular integrales definidas.

Saludos

;)

;)

Muchas Gracias!

¿Siempre debe ser así para plantear la derivada? Porque yo la había plateado como

$$\begin{align}&\int_{-1}^3{x^2-3-2x \ \ dx}\end{align}$$

pero me da negativo el resultado para  el area,

Está bien planteada, pero como te digo el área es el valor absoluto. Si el cálculo lo has hecho bien te dará lo mismo pero negativo. Entonces tomas el valor absoluto de ese número.

Es bastante tedioso esos cálculos