Anónimo
Sumas de Riemann y calculo de área con integrales?
Aproxime:
$$\begin{align}&\int _1^2\:\frac{1}{1+x^4}\end{align}$$utilizando las sumas de Riemann del punto izquierdo con n = 8
1 Respuesta
Respuesta de Lucas m
1
;)
Hola Juan Valencia!
La suma de Riemann izquierda se calcula como:
$$\begin{align}&\int_a^bf(x)dx \simeq \sum_{i=0}^{n-1} f(x_{i-1}) \Delta x= \Delta x \sum_{i=0}^{n-1} f(x_{i-1})\\&\\&\Delta x= \frac {b-a} n= \frac{2-1} 8= \frac 1 8\\&Intervalos:\\&[1, \frac 9 8]==> f(1)= \frac 1 2\\&\\&[ \frac 9 8, \frac{10} 8] ==> f( \frac 9 8)=\frac{4096}{10657}\\&\\&[ \frac{10} 8, \frac {11} 8]==> f( \frac{10} 8)=\frac {256}{881}\\&\\&[\frac {11} 8, \frac{12} 8]==> f( \frac{11} 8)= \frac{4096}{18737}\\&\\&[ \frac {12} 8, \frac{13} 8]==> f(\frac{12} 8)=\frac{16}{97}\\&\\&[\frac{13} 8, \frac{14} 8]==> f(\frac{13} 8)=\frac{4096}{32657}\\&\\&[ \frac {14} 8, \frac{15} 8]==> f( \frac{14} 8)=\frac{256}{2657}\\&\\&[\frac {15} 8,2] ==>f( \frac{15} 8)= \frac{4096}{54721}\\&\\&\int_1^2 \frac 1 {1+x^4}dx \simeq \Delta x \Big[ f(x_0)+f(x_1)+f(x_2)+········+f(x_7) \Big]=\\&\\&\frac 1 8 (1.855107126)=0.23188839\end{align}$$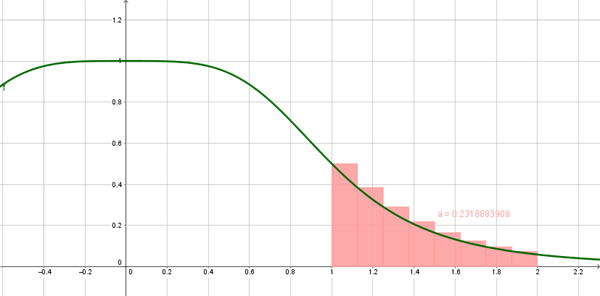
Saludos
;)
;)