Grafica y analiza la siguiente funcion
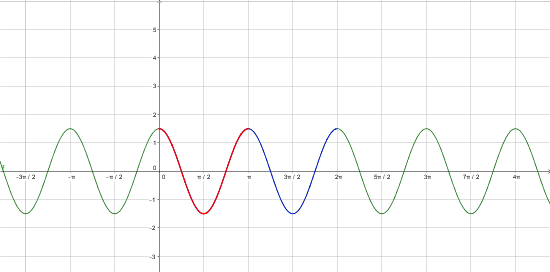
- Graficá y analizá la función: y = 3/2 cos (2x)
- Analizá cada afirmación e indicá si es verdadera o falsa:
- a) Para x = pi/4 se cumple que senx = cosx
- b) x = pi/4 es la única solución de la ecuación senx = cosx
- c) No existe ningún valor de x para el cual senx = 1,85
- d) No existe ningún valor de x para el cual tgx = 1,85
- Hallá los valores de x que satisfacen la ecuación dada en un giro: cos"2x-3cosx=-2
1 respuesta
Respuesta de Lucas m
1