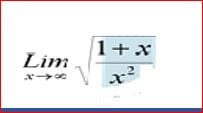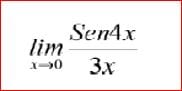Compartamos ideas para aprender más

Son muchas consultas para una sola pregunta. Te dejo las primeras dos

$$\begin{align}&\lim_{x \to 3} 2x-8\\&\text{Por ser un polinomio (que es continuo) directamente evaluamos en el punto}\\&\lim_{x \to 3} 2x-8 = 6-8=-2\\&---\\&\lim_{n \to 0} \frac{\sqrt{5+n}-\sqrt{5}}{\sqrt{2n}}\\&\text{Multiplicamos por el conjugado, buscando eliminar la raíz}\\&\lim_{n \to 0} \frac{\sqrt{5+n}-\sqrt{5}}{\sqrt{2n}}=\lim_{n \to 0} \frac{\sqrt{5+n}-\sqrt{5}}{\sqrt{2n}}\cdot \frac{\sqrt{5+n}+\sqrt{5}}{\sqrt{5+n}+\sqrt{5}}=\\&\lim_{n \to 0} \frac{(\sqrt{5+n})^2-(\sqrt{5})^2}{\sqrt{2n}(\sqrt{5+n}+\sqrt{5})}=\lim_{n \to 0} \frac{5+n-5}{\sqrt{2}\sqrt{n}(\sqrt{5+n}+\sqrt{5})}=\\&\lim_{n \to 0} \frac{n}{\sqrt{n}(\sqrt{2(5+n)}+\sqrt{2\cdot 5})}=\\&\lim_{n \to 0} \frac{\sqrt{n}}{(\sqrt{10+2n}+\sqrt{10})} \to \frac{0}{2 \sqrt{10}} = 0\end{align}$$

Espera a que otro experto te responda las otras dos, o haz una nueva pregunta

Salu2