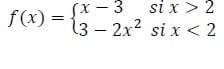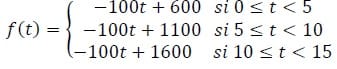Ejercicio sobre limites en matemáticas
Momento 2.
- Elabora una gráfica de la función que se indica en seguida (no deberá incluir la gráfica en su trabajo), y conteste lo siguiente:
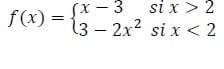
- a) ¿Por cuál valor de𝑦 atraviesa la función el eje de las ordenadas? O sea la ordenada al origen.
- b) Determina los límites cuando𝑥 tiende a 2.
- c) Indica si la función es continua precisamente en𝑥=2. Explica en breves palabras.
- La siguiente expresión representa niveles de inventario de cierto producto en su empresa, en diferentes tiempos. (Sugerencia: también grafícala por separado, sin incluirla.)
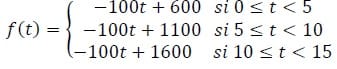
Contesta lo siguiente:
- a) ¿Es continua la función en 𝑡=2? Explica por qué y determina su valor.
- b) ¿Es continua la función en 𝑡=5? Determina el límite cuando “x” tiende a 5 en las dos primeras secciones de la función, y contesta la pregunta.
c) ¿Es continua la función en 𝑡=15? Demuéstralo
1 respuesta
Respuesta de Lucas m
1
;)
Hola Alver!
Hacemos un problema de esos por pregunta.
Te hago el primero y manda el otro en otra pregunta o espera otro experto
2a) f(0)=3-0=3
b)
$$\begin{align}&\lim_{x\to 2^-}f(x)=\lim_{x\to 2^-}3-2x^2=3-8=-5\\&\lim_{x\to 2^+}f(x)=\lim_{x\to 2^+}x-3=2-3=-1\\&\\&\text{Una función es continua en un punto si}\\&\\&\lim_{x\to 2^-}f=\lim_{x\to 2^+}f=f(2)\end{align}$$Esta función ni tiene límite en x=2, ya que los límites laterales no coinciden, y además tampoco tiene imagen enx=2 .No existe f(2) por no estar definida en ese valor
Se llama una Discontinuidad de salto
;)
;)
||*||
;)
