Como se demuestra el siguiente enunciado
- En un cuadrado de lado 3 se cortan triángulos rectángulos isósceles en cada una de sus cuatro esquinas, de tal manera que se forma un octágono regular al interior del cuadrado. Demostrar que el área de este octágono se puede expresar como 18 − 18
1 Respuesta
Hay un evidente error en la consigna, ya que expresar el área del octógono como 18-18 sólo daría la posibilidad de área=0, lo que no es real.
Si el octógono es regular, todos los lados son iguales, por lo que la hipotenusa de cada triángulo isósceles será igual al lado del octógono sobre el cuadrado.
Lado del cuadrado=L=3;
Lado del octógono=hipotenusa del triángulo isósceles=x;
Lados iguales del triángulo isósceles=y.
L=x+2y; o: x+2y=3;
Área total del cuadrado ( A(c) )= L^2 = 9 unidades^2.
Por Pitágoras: x^2=y^2+y^2; x^2=2y^2; x=y*√2; reemplazo en x+2y=3:
y*√2 + 2y = 3; despejo y: y*(2+√2)=3;
y= 3/(2+√2);
Como cada triángulo isósceles es a su vez rectángulo, su área (A(t) ) será:
A(t) = y^2 /2; o: A(t) = 9/[2* (2+√2)^2]; o: (9/2) / (2+√2)^2
Y al tener cuatro triángulos iguales, el área del octógono (A(o) ) puede expresarse como:
A(o) = A(c) - 4*A(t);
A(o) = 9 - [4* (9/2) / (2+√2)^2];
A(o) = 9 - [18/ (4+4√2+2)]; o: A(o) = 9 - [18/ (6+4√2)]
A(o) = 9 - {18/ [2*(3+2√2)]};
A(o) = 9 - [9/(3+2√2)]; o: 9* {1-[1/(3+√2)]}; o: 9* (3+√2-1)/(3+√2);
A(o) = 9* (2+√2) / (3+√2);
A(o) = 6.9611 unidades^2; que es el área del octógono regular inscrito en un cuadrado de 3 unidades de lado.
También podría haberse hecho de esta forma, teniendo en cuenta que los cuatro triángulos rectángulos equivalen a 2 cuadrados de lado y:
A(o) = 9 - 2y^2; reemplazo:
A(o) = 9 - 2*[3/(2+√2)]^2;
A(o) = 9 - [18/(2+√2)^2]; y siguiendo como está explicado anteriormente.
El área esta dada por
$$\begin{align}&18\sqrt{2}-18\end{align}$$perdon por el error en el enunciado. Podrias explicarme nuevamente, si fueras tan amable.
Si todo es correcto, debería darse la igualdad:
9 - [18/(2+√2)^2] = 18√2 -18; intentemos:
27= 18√2 + 18/(2+√2)^2;
27 = 18 * {√2 + [1/(2+√2)^2]};
3/2 = {√2* [(2+√2)^2 + 1]} / (2+√2)^2;
(3/2)*(2+√2)^2 = √2 * (4+4√2+2 +1);
(3/2) * (4+4√2+2) = √2 * (7+4√2);
3* (3+2√2) = 7√2 + 8;
9 + 6√2 = 7√2 + 8;
1 =√2; lo que es incorrecto.
Revisemos todas las consignas:
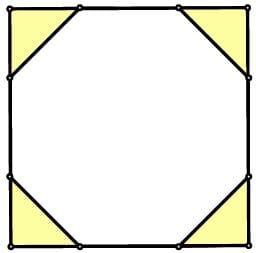
Lado del cuadrado=L=3;
Lado del octógono=hipotenusa del triángulo isósceles=x;
Lados iguales del triángulo isósceles=y.
L=x+2y; o: x+2y=3;
Área total del cuadrado ( A(c) )= L^2 = 9 unidades^2.
Por Pitágoras: x^2=y^2+y^2; x^2=2y^2; x=y*√2;
reemplazo en x+2y=3:
y*√2 + 2y = 3; despejo y: y*(2+√2)=3;
y = 3 / (2+
Lado del cuadrado=L=3;
Lado del octógono=hipotenusa del triángulo isósceles=x;
Lados iguales del triángulo isósceles=y.
L=x+2y; o: x+2y=3;
Área total del cuadrado ( A(c) )= L^2 = 9 unidades^2.
Por Pitágoras: x^2=y^2+y^2; x^2=2y^2; x=y*√2; reemplazo en x+2y=3:
y*√2 + 2y = 3; despejo y: y*(2+√2)=3;
y = 3/(2+
Lado del cuadrado=L=3;
Lado del octógono=hipotenusa del triángulo isósceles=x;
Lados iguales del triángulo isósceles=y.
L=x+2y; o: x+2y=3;
Área total del cuadrado ( A(c) )= L^2 = 9 unidades^2.
Por Pitágoras: x^2=y^2+y^2; x^2=2y^2; x=y*√2; reemplazo en x+2y=3:
y*√2 + 2y = 3; despejo y: y*(2+√2)=3;
y=3/(2+
Lado del cuadrado=L=3;
Lado del octógono=hipotenusa del triángulo isósceles=x;
Lados iguales del triángulo isósceles=y.
L=x+2y; o: x+2y=3;
Área total del cuadrado ( A(c) )= L^2 = 9 unidades^2.
Por Pitágoras: x^2=y^2+y^2; x^2=2y^2; x=y*√2; reemplazo en x+2y=3:
y*√2 + 2y = 3; despejo y: y*(2+√2)=3;
y = 3 / (2+√2);
El área total de los cuatro triángulos rectángulos (equivalente a 2 cuadrados de lado y) es: A(t) = 2y^2;
A(t) = 18/ (2+√2)^2;
Ao = Ac - At;
Ao= 9 - 18/ (2+√2)^2; corroborando que este cálculo es correcto.
