Determinar La curva de nivel

;)
Hola karla!
Las curvas de nivel salen de hacer z=constante

$$\begin{align}&a)\\&z=x+y-2\\&\\&x+y-2=k  \Rightarrow y =-x+(k+2)\\&\text{son rectas paralelas}\\&k=0  \Rightarrow y=-x+2\\&k=1 \Rightarrow y=-x+3\\&\\&\\&k=-10 \Rightarrow y=-x-8\end{align}$$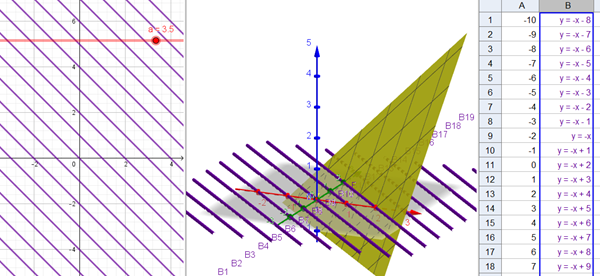

Las rectas de nivel de un plano son rectas

b)

$$\begin{align}&-x^2y^2=k  \Rightarrow y^2 =\frac k{-x^2} \Rightarrow y= \pm \sqrt {\frac k { -x^2}} = \pm \frac c  x\\&\\&\text{solo existen para k negativos, son hipérbolas equiláteras}\\& \text{excepto para k=0,que es la recta y=0}\\&\\&k=-10 \Rightarrow y= \pm \frac{ \sqrt {10}} x\\&\\&k=-1 \Rightarrow y= \pm  \frac 1 x\\&\\&k=0  \Rightarrow y=0\end{align}$$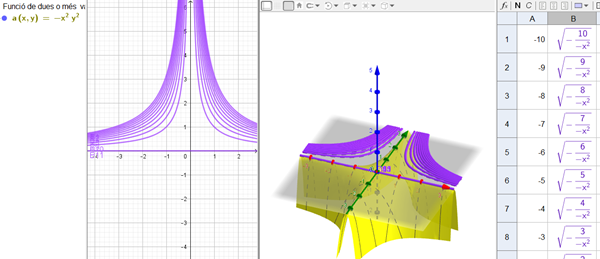

Saludos

;)

||*||