Como resuelvo este ejercicio de estudio de funciones
Como hallo la curvatura, el punto de inflexión, mínimos y máximos locales.
1 Respuesta
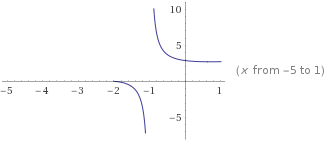
Analiza desde x>( - infinito) hasta x = 2 no esta definida porque el denominador - función logarítmica - no tiene solución real en este intervalo infinito.
Partiendo de x>2.. la función es (-) por la izquierda creciente hasta (- infinito) para x= -1. Por la derecha la función es (+) creciente cuando x tiende a (-1).
Hay una discontinuidad no evitable en x= -1.
Como para x>-1 la función es decreciente pero para x tendiendo a infinito la función también tiende a infinito... debe haber un mínimo relativo.
Derivando f(x) te esta quedando: df/dx = (lg(x+2) + 1) / log^2(x+2) ............que si la anulas llegarias a que x( min. relativo) = 0.7181.
Resumiendo: La función esta definida para x mayor que (-2)... tomando valores negativos.
Tiene una discontinuidad no evitable en x= -1. A partir de alli Pasa a ser (+) en todo el dominio de x hasta + infinito.
Presenta un minimo relativo para x= 0.7181. ( exactamente = e - 2).
