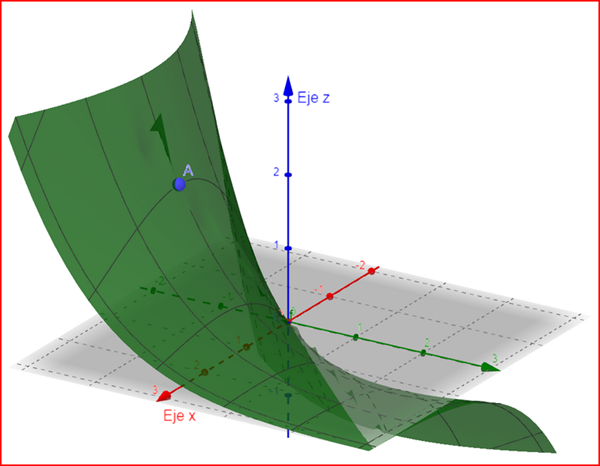
No se como resolver este problema de continuidad en varias variables
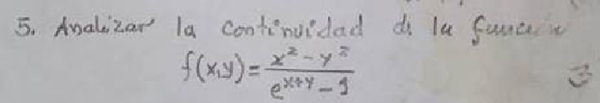
...
3 Respuestas
Respuesta de Karl Mat
Respuesta de Mario Rodríguez
2
Respuesta de Norberto Pesce