3. Hallar la ecuación de la recta que pasa por el punto C y es perpendicular a la recta que pasa por los puntos A y B. Graficar
A(-1,6); B(-2,-5); C(2,-7)
Necesito de su amable colaboración con este tema .
1 Respuesta
Hallas la pendiente de AB
$$\begin{align}&M=\frac{Yb-Ya}{Xb-Xa}\end{align}$$Con ella haces uso que Dos rectas son perpendiculares si la multiplicacion de sus pendientes=-1
Tienes una pendiente hallas la otra, luego con esa pendiente y el punto C haces uso de la ecuación punto pendiente (Y-Yc)=M'(X-Xc)
¡Gracias!
De acuerdo a los resultados obtenidos, ¿cómo se utiliza los resultados para realizar la gráfica?
Graficas los puntos A, B y C. Uniendo los puntos A y B obtienes la recta. Y luego con la ecuación de la recta perpendicular insertas un valor x cualquiera, obtendrás un valor de y, graficas ese punto y lo unes con C
¿Osea tomo la ecuación de respuesta obtenida por medio del punto pendiente?
Exacto
Tengo la ecuación, ¿ahora la cojo y la soluciono para el obtener el punto?
¿Cómo te dio la ecuación de la recta?
9x -3y-5= 0
No está bien, veamos
¿Me podría indicar en donde se encuentra el error?
Pendiente recta AB
A(-1,6); B(-2,-5)
$$\begin{align}&M_1=\frac{-5-6}{-2-(-1)}=11\\&\\&\end{align}$$Pendiente recta perpendicular
M
$$\begin{align}&M_2M_1=-1\\&M_2*11=-1\\&M_2=\frac{-1}{11}\end{align}$$Ecuación pto pendiente usando el punto C C(2,-7)
$$\begin{align}&(Y-(-7))=\frac{-1}{11}(X-2)\\&11Y+77=-X+2\\&X+11Y+75=0\end{align}$$
¿Encontraste tu error?
Si ya, ¿ahora tomo esa ecuación de pto pendiente y ahora como la remplazo? Para hallar el ultimo punto que una a C
Hmm bueno te recomiendo x=0 que es el más sencillo, eso si, te va a dar un valor medio raro, -75/11
O sea que -75 /11 lo uno con c y ahí se me halla el punto de intersección
Si, aunque si quieres hallar el punto de intersección exacto debes hallar la ecuación de la recta AB y luego hacer un sistema de ecuaciones entre ambas rectas, el valor de x e y van a ser las coordenadas de la intersección
¿No seria que en la pendiente recta perpendicular es 11 y no -1/11 ya que se podría invertir la fracción y cambiando el signo?
Hay que usar la pendiente 11 y el punto A(o B, es indiferente) en la ecuación punto pendiente.
Me dice el tutor que verifique la ecuación solicitada . Al parecer tiene error
X+11Y+75=0
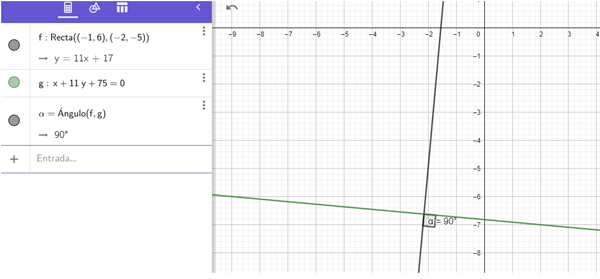
La recta g es la que se encuentra el pto C
La recta f y=11x+17 es la que pasa por a y b
Podemos comprobar sustituyendo sus coordenadas
2+11(-7)+75=0, si se cumple que es cero asi que se encuentra en la recta
Otra forma de verlo es que si tomas solo los valores de x e y de ambas rectas (el termino independiente lo que hace es desplazarlo, no lo gira)
Tenemos para la recta f eliminando el termino independiente y-11x=0
Que en forma de vector es (-11,1)
Y en el caso de la recta g (1,11)
Si hacemos el producto escalar (-11,1)(1,11)=-11*1+1*11=0 , el producto escalar entre dos vectores es cero si son perpendiculares, asi que las rectas son perpendiculares. Lo unico que habria que probar es que a y b pertenecen a la recta f, y si lo hacen.
El resultado està bien
