Ok, asumiendo que está bien lo que hiciste, entonces intentaremos triangular la matriz, pare esto haremos la fila 2 igual a la fila 2 anterior menos 2 veces la fila 1 y a la fila 3 igual a la fila 3 anterior menos la fila 1, esto hace que la matriz resultante quede...
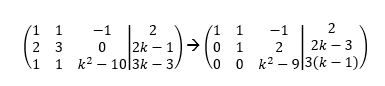
La matriz ya está triangulada, ahora queda ver las consignas:
a) Tenga solución única, para esto el término k^2 - 9 debe ser distinto de 0, o sea
k^2-9 <> 0
(k-3)(k+3) <> 0
K debe ser distinto de 3 y de -3
b) no tenga solución
Para eso tiene que haber un absurdo en alguna de las filas, por ejemplo llegar a algo del estilo
1 = 2
Ya sabemos que ocurre para los valores de k distinto de +/- 3, veamos ahora que pasa para esos dos valores
k=3, entonces la última fila queda
0 = 3 * 2 = 6 Absurdo! (esto es lo que pedía el punto y es un valor de k que cumple que el sistema no tiene solución
ahora veamos el otro caso
k = -3, queda
0 = 3 * (-4) = -12 también es absurdo
Por lo tanto para k = +/-3 el sistema es indeterminado (no tiene solución)
Ya revisamos todos los valores posibles de k, por lo tanto no hay ningún valor, para el cual el sistema tenga soluciones múltiples.
Salu2




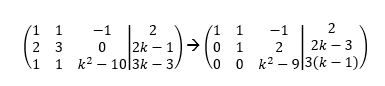

 sdfsdf
sdfsdf
La cuestión es que no está bien lo que hizo, olvidó poner la k - Alejandro Salazar
y bueh...:-) - Anónimo