Usaré coordenadas esféricas, anexaré imagen para que sepas cuales son los ángulos que usaré
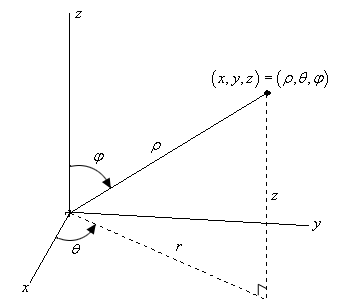
Recuerda que al hacer el cambio a coordenadas esfericas nos queda
$$\begin{array}{c}x = \rho \sin \varphi \cos \theta \hspace{0.25in}y = \rho \sin \varphi \sin \theta \hspace{0.25in}z = \rho \cos \varphi
{x^2} + {y^2} + {z^2} = {\rho ^2} \hspace{0.25in}
dV = {\rho ^2}\sin \varphi \,d\rho \,d\theta \,d\varphi
\end{array}$$Las curvas de arriba y abajo son esferas de ecuaciones
$$\begin{align}&z^2+x^2+y^2=1\\&z^2+x^2+y^2=4\end{align}$$La del medio es un cono
$$\begin{align}&\frac{z^2}{3}=x^2+y^2\end{align}$$Vamos a usar sustituir el valor de x^2+y^2 del cono en la esfera de radio 1 (como el radio es 1 rho=1)
$$\begin{align}&\frac{z^2}{3}+z^2=1\\&z^2+3z^2=3\\&z=\frac{\sqrt{3}}{2}\\&\rho \sin \varphi=\frac{\sqrt{3}}{2}\\&\rho=1\\&\sin \varphi=\frac{\sqrt{3}}{2}\\& \varphi= \frac{\pi}{3}\end{align}$$Es decir el angulo que forma el cono con el eje z es pi/3, y como el cono es "recto", el angulo no varia.
Tenemos entonces
$$\begin{align}&1 \leq \rho \leq 2\\&0 \leq \varphi \leq \frac{\pi}{3}\\&0 \leq \theta \leq 2 \pi\end{align}$$Rho va de 1 a 2 ya que son los radios de las esferas que son las tapas de nuestro "cono truncado", y phi va de 0 a pi/3 para que cubra todo ese volumen del cono, ya tenemos todo listo, la integral es bastante sencilla ya que nos piden el volumen nos queda. Te doy el resultado pero creo que sabras como hallarlo
$$\begin{align}&\int \int \int dV= \int_{0}^{\frac{\pi}{3}}{{\int_{0}^{2 \pi}{{\int_{1}^{2}{{{\rho ^2}\sin \varphi \,\,d\rho }}\,d\theta }}\,d\varphi }}= \frac{7 \pi }{3}\end{align}$$



