Como se hace la siguiente funcion de valor absoluto Gráfico f(x)=|x+1|+|x-1| con su dominio y rango

Evaluemos las funciones por separado.

|x+1| es cero cuando x=-1, y |x-1| es cero cuando x=1. El dominio es claramente todos los reales puesto que no hay niguna restriccion en los valores absolutos.

Ese dominio vamos a dividirlo en pedazos, en aquellos valores donde vimos que cada valor absoluto es cero.

NOTA: Puse los intervalos con paréntesis, pero va con corchetes

Los intervalos nos queda entonces (-inf,-1),(-1,1),(1, inf). La razón por la cual estamos dividiendo los intervalos es debido a que hay que recordar que el valor absoluto es una especie de función por partes que se toma positivo a veces y en otras negativos.

En el primer intervalo (-inf,-1) en |x+1| se toma -(x+1) y en |x-1| se toma -(x-1). Reemplazandolo en nuestra funcion nos queda  -x-1-x+1=-2x, que es una recta con pendiente -2

Ahora en el segundo intervalo (-1,1) |x+1| es positivo y |x-1| es negativo por lo que se toma (x+1) y --(x-1) respectivamente, sustituyéndolo en la función nos queda

(x+1)-(x-1)=2, una recta horizontal

 Y en el ultimo intervalo nos queda que tanto |x+1| como |x-1|son positivos por lo que quedan (x+1) y (x-1), reemplazandolo en la funcion

(x+1)+(x-1)=2x, una recta de pendiente 2. Cual es el rango, pues  vamos a graficar las rectas que obtuvimos

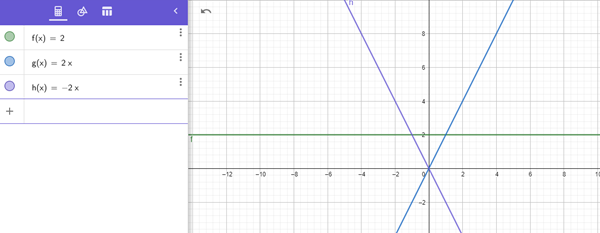
Recuerda, la recta -2x que es la morada va en el intervalo (-inf,-1], luego la recta 2 va de [-1,1] y la recta 2x va desde 1 hasta infinito. De ahí claramente vemos que el rango seria [2,+infinito).

Te muestro imagen de la función original

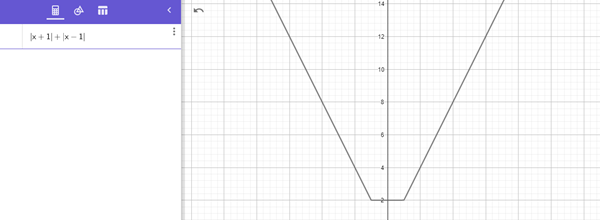
Es lo que tuvimos