Para el 20, primero voy a poner unas letras para identificar los ángulos y triángulos que se forman en la imagen
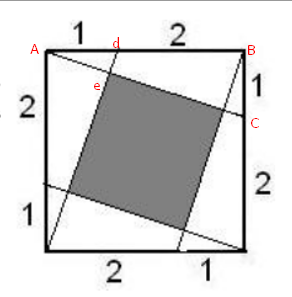
Además creo que se ve 'fácil' que los triángulos grandes (ej/ ABC) son congruentes a los triángulos pequeños (e/ Aed) ya que tienen 2 ángulos en común, por lo tanto el tercero también mide lo mismo y por lo tanto los lados son proporcionales. Dicho esto voy a pasar a calcular cuanto mide el lado del cuadrado sombreado (supongo que hay otros métodos, pero por lo pronto no se me ocurre ninguno :))
$$\begin{align}&\text{Lo primero que voy a calcular es el lado AC, que sale por Pitágoras y es}\\&AC = \sqrt{10}\\&\text{Ahora calculo Ae, usando la proporcionalidad de los triángulos}\\&\frac{Ae}{AB}=\frac{Ad}{AC} \to Ae = \frac{3 \cdot 1}{\sqrt{10}}=\frac{3 \sqrt{10}}{10}\\&\text{Ahora calculo 'de', para restárselo al valor de AC}\\&\frac{de}{BC}=\frac{Ad}{AC} \to de = \frac{1 \cdot 1}{\sqrt{10}}=\frac{\sqrt{10}}{10}\\&\text{Ahora sí, el lado del cuadrado de color, digamos X, es:}\\&X= AC - Ae - de = \sqrt{10} - \frac{3 \sqrt{10}}{10}- \frac{\sqrt{10}}{10}=\frac{3 \sqrt{10}}{5}\\&\text{Por lo tanto el área sombreada será}\\&X^2 = \bigg(\frac{3 \sqrt{10}}{5} \bigg)^2=\frac{9 \cdot 10}{25}=\frac{18}{5}\\&\text{Ahora veamos en porcentaje, cuanto es}\\&\frac{X^2}{C} = \frac{18/5}{9}=\frac{2}5=0.4 = 40\%\\&\\&\end{align}$$Opción, D)
Salu2





Gracias profesor pero me piden el desarrollo de los problemas y la verdad que mucho no lo entiendo;usted lo puede hacer así después estudio el desarrollo por favor? - maria mustacciolo
Profesor lo he resuelto con los 400 km primero y con los 600 km después y he obtenido los siguientes resultados para que usted me diga si están bien:La empresa A cobra 575 por 400km y 675 por 600 kmLa empresa B cobra 550 por 400 km y 700 por 600 kmLa empresa C cobra 554 por 200km y 758 por 400 kmPor lo tanto la empresa A es la más económicaEstará bien profesor?? - maria mustacciolo
Tenés que llegar a dos conclusiones: si piensa realizar 400km, entonces conviene la empresa B, mientras que si piensa viajar 600km la que conviene es la empresa A (eso lo podés ver en la imagen que te dejé también). Otra forma más completa de dar la respuesta es decir entre que valores va conviniendo cada empresa (mirando en el gráfico entre 400 y 600km, cual es la curva que va por abajo en cada intervalo). - Anónimo
Muchas gracias profesor por ayudarme!!!es usted muy amable!!! - maria mustacciolo
Me puedas ayudar con el 20 y el 21?por favor! - maria mustacciolo
Profesor por favor ya he resuelto todos solo me quedo sin resolver el número 20 por favor me puede ayudar!!!!! - maria mustacciolo
Excelente profesor muchas gracias!!!! - maria mustacciolo