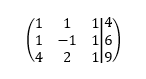Regla de cramer para encontrá rlos coeficientes de un polinomio
Use la regla de cramer para encontrar los coeficientes a, b, c del polinomio cuadrático p(x)= x²+bx+c, que pasa por los puntos (1, 4 ),(-1,6) y (2,9)
1 respuesta
Supongo que en p(x) te faltó el término 'a'
Primero reemplazamos los valore de los puntos dados...
(1,4)
a + b + c = 4
(-1,6)
a - b + c = 6
(2,9)
4a + 2b + c = 9
O sea que la matriz que queda para analizar es
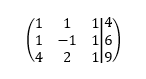
El determinante de la matriz A (parte izquierda de la vista anterior) es:
(Desarrollo por primer fila)
Det = 1*(-1*1 - 2*1) - 1 * (1*1-4*1) + 1 * (1*2-4*(-1)) = -3 + 3 + 6 = 6
Para 'a' reemplazamos la primer columna por la columna de resultados (parte derecha de la imagen que puse)
Det a = 12
Haciendo lo mismo para b, c queda
Det b = -6
Det c = 6
Por lo que los valores de a,b,c serán respectivamente
a = Det a / Det = 12 / 6 = 2
b = Det b / Det = -6 / 6 = -1
c = Det c / Det = 6 / 6 = 1
Así que el polinomio P(x) = 2x^2 - x + 1
Salu