Como puedo encontrar un VECTOR ortogonal a 'u' y 'v'
Como puedo encontrar un vector ortogonal a 'u' y 'v' que tenga norma 
u=(2,13,-7,5) u=(1,7,-3,6)
He podido encontrar los valores w1, w2, w3, w4 por medio del escalonamiento, pero no entiendo después de esta parte que debo hacer.
1 Respuesta
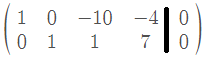
Respuesta de Alejandro Salazar
2
El span del espacio nulo es
<(10,-1,1,0),(4,-7,0,1)>
Los vectores de ese subespacio los podemos escribir como s(10,-1,1,0)+t(4,-7,0,1)
La norma de esos vectores son
$$\begin{align}&|w|=\sqrt{s^2(102)+t^2(66)}=3 \sqrt{2}\\&\text{Asumamos un valor de s cualquiera, digamos 0}\\&\sqrt{66t^2}=3 \sqrt{2}\\&t=\frac{\sqrt{33}}{11}\\&\\&\text{Nuestro vector seria una combinacion lineal con s=0 y t el valor }\\&\text{que conseguimos}\\&w=\frac{\sqrt{33}}{11}(4,-7,0,1)\end{align}$$Como notas, hay infinitas soluciones
