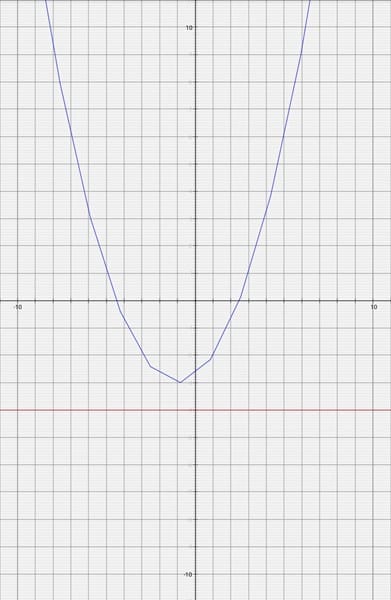
1. Obtén la ecuación ordinaria, los elementos y traza la gráfica de la parábola cuya ecuación general es: x2 + 2x – 4y -11 = 0

Verónica por paso

1)Identificación; la ecuación de la parábola esta casi completa respecto a la variable por por ello, representa una parábola cuyo eje es paralelo al eje y cuya característica de ecuación ordinaria es

$$\begin{align}&(x-h)^2=4p(y-k)\end{align}$$

 2)-obtención; completando cuadrados respecto a la variable x tenemos 

¿Entonces cuál es la ecuación ordinaria? Me lo podrías explicar otra vez por favor, con su procedimiento de como lo sacaste por favor

Continuación

$$\begin{align}&x^2+2x-4y-11=0\\&x^2+2x+(\frac{2}{2})^2-4y-11-(\frac{2}{2})^2=0\\&(x+1)^2-4y-12=0\\&(x+1)^2=4y+12\\&(x+1)^2=4(y+3)\end{align}$$

Por lo que se puede apreciar el vértice tiene las coordenadas v(-1,-3), como se cumple que 4p=4 de donde p=1>0 por ello la parábola abre hacia arriba 

Calculo del foco debe cumplir que f(-1,-3+p)=f(-1,-3+1)=f(-1,-2)

La ecuación de la directriz es y=-3-p de donde y=-3-1=-4

Y la longitud del lado recto es |4p|=4

Un favor me podría mandar la gráfica ya hecha por favor