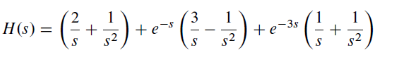El primer término en paréntesis en directo. Para los otros dos tienes que recordar que
$$\begin{align}&\mathcal{L}\{u(t-a)\} = e^{-as}\frac{1}{s}\end{align}$$Para los dos terminos siguientes puedes proceder de varias formas pero en definitiva vas a tener que aplicar la transformada de la convolución. La forma más sencilla (a ojo) es primero hacer la distributiva, de esa forma los términos con 1/s son directamente la transformada de la función escalón y solo te quedarían los términos de la forma
$$\begin{align}&e^{-as}\frac{1}{s^2} = \left[e^{-as}\frac{1}{s}\right] \frac{1}{s}\end{align}$$que reconoces como el producto de transformadas, y la antitransformada sería el producto de convolución, por lo que tienes que resolver la integral.