Va de mecánica
Hola,
Te agradecería que me ayudases en la siguiente cuestión ... No la consigo resolver
Se trata de un bloque de 2 g de masa que se halla inicialmente en reposo en el punto más alto de un hemisferio liso de 20 cm de radio.
Al desplazarlo ligeramente de su posición de equilibrio, comienza a caer deslizándose sobre el hemisferio. Calcular el ángulo donde el bloque se separará del hemisferio ( se desprecia el rozamiento).
Te agradecería que me ayudases en la siguiente cuestión ... No la consigo resolver
Se trata de un bloque de 2 g de masa que se halla inicialmente en reposo en el punto más alto de un hemisferio liso de 20 cm de radio.
Al desplazarlo ligeramente de su posición de equilibrio, comienza a caer deslizándose sobre el hemisferio. Calcular el ángulo donde el bloque se separará del hemisferio ( se desprecia el rozamiento).
1 respuesta
Respuesta de derinsekt
1
1

Este es un problema muy clásico, recordemos que el momento en que el objeto se separa de la esfera la fuerza normal se hace cero, sabemos que sobre el objeto actúan dos fuerzas, la fuerza de gravedad que es mg (g:aceleración de la gravedad en la superficie de la tierra) y la fuerza normal N que es perpendicular al punto donde se tocan el objeto y la esfera, mientras el objeto toque el hemisferio, N va en dirección radial, así que seria bueno conocer la fuerza total en dirección radial, como la gravedad empuja hacia abajo, la componente radial con respecto del centro del hemisferio es -mgSen(T), donde T es el angulo que forman la superficie en la que se encuentra el hemisferio y la posición del objeto. Estas dos fuerzas tienen que igualarse a la fuerza centrípeta, que como mantiene al objeto pegado al hemisferio es negativa, y es -mv^2/r, como el objeto inicialmente se mueve sobre la esfera, r=R, y la fuerza centrípeta es -mv^2/R, así que:
-mv^2/R=N-mgSen(T)
N=m(gSen(T)-(v^2/R))
Entonces ahora nos falta v^2, pero como no hay fricción, la energía se conserva, entonces, la energía potencial inicial era de U=mgR y la energía potencial para cierto U(T)=mgRSen(T), la energía cinética es la diferencia entre ambos entonces
mv^2/2=mgR(1-Sen(T))
mv^2=2mgR(1-Sen(T))
Que podemos sustituir en la ecuacion que teniamos desde antes
N=mgSen(T)-(2mgR(1-Sen(T))/R)
N=mg(Sen(T)-2(1-Sen(T)))
N=mg(3Sen(T)-2)
Y como dije antes, en el instante en que se separa el objeto del hemisferio, N se hace cero entonces
Sen(T)=2/3
Supongo que podrás obtener de aquí el angulo, solo aplica la función inversa de Seno (Sen^-1 o ArcSen, como la conozcas)
Cualquier duda, puedes preguntar
-mv^2/R=N-mgSen(T)
N=m(gSen(T)-(v^2/R))
Entonces ahora nos falta v^2, pero como no hay fricción, la energía se conserva, entonces, la energía potencial inicial era de U=mgR y la energía potencial para cierto U(T)=mgRSen(T), la energía cinética es la diferencia entre ambos entonces
mv^2/2=mgR(1-Sen(T))
mv^2=2mgR(1-Sen(T))
Que podemos sustituir en la ecuacion que teniamos desde antes
N=mgSen(T)-(2mgR(1-Sen(T))/R)
N=mg(Sen(T)-2(1-Sen(T)))
N=mg(3Sen(T)-2)
Y como dije antes, en el instante en que se separa el objeto del hemisferio, N se hace cero entonces
Sen(T)=2/3
Supongo que podrás obtener de aquí el angulo, solo aplica la función inversa de Seno (Sen^-1 o ArcSen, como la conozcas)
Cualquier duda, puedes preguntar

Hola,
Si N va en dirección radial... significa que va en la dirección del radio y por tanto en dirección de Py (el peso se descompone en px y py)... pero lo que nos interés calcular es Px ->Px=P*sen(T)... ¿esto es correcto?
por tanto P*cos(T)-FN=Fcp--->(FN=fuerza normal=O)....no es correcto el cos si no el sen.
Para ver el dibujo de las coordenadas y el ángulo al que me refiero :
http://www.scribd.com/doc/17054369/dinamica-t2
En la expresión: -mgsen(T) ... no entiendo por qué aparece el signo negativo...
Muchísimas gracias
Si N va en dirección radial... significa que va en la dirección del radio y por tanto en dirección de Py (el peso se descompone en px y py)... pero lo que nos interés calcular es Px ->Px=P*sen(T)... ¿esto es correcto?
por tanto P*cos(T)-FN=Fcp--->(FN=fuerza normal=O)....no es correcto el cos si no el sen.
Para ver el dibujo de las coordenadas y el ángulo al que me refiero :
http://www.scribd.com/doc/17054369/dinamica-t2
En la expresión: -mgsen(T) ... no entiendo por qué aparece el signo negativo...
Muchísimas gracias

No, el problema es que en un plano inclinado, tu objeto solo se mueve en una dirección, entonces puedes definir tu sistema de coordenadas de acuerdo al objeto, lo que hace muy fácil dividir el peso en sus componentes y obtener la velocidad, pero si tu objeto esta cayendo sobre una superficie circular, las coordenadas más correctas no son las cartesianas, y menos tomadas con respecto de tu objeto, puesto que el objeto esta cambiando de dirección a cada instante.
¿Entonces qué es lo más correcto? Puesto que el problema trata unicamente desde el momento en que el objeto comienza a moverse y hasta que se desprende de la superficie hemisferica, el movimiento que hace es circular, así que las coordenadas más correctas son las polares (radio y angulo), y escogemos como el origen al centro de la hemisfera (si fuera una esfera completa) y el angulo corresponde al angulo que hace la posición del objeto con respecto de la superficie donde esta el hemisferio, a la energía no le importa las coordenadas que uses, así que usamos las mismas energías potencial, cinética y total; ahora no tenemos que dividir la fuerza normal en componentes, ya que la fuerza normal siempre va en dirección radial, y la fuerza centrípeta ya la tenemos, como usamos coordenadas polares la fuerza centrípeta esta en función de R y no de (x+y)^1/2, entonces solo falta encontrar la componente del peso en dirección radial, el peso siempre apunta hacia abajo, así que en coordenadas cartesianas el peso es -mg en dirección de "y" (el "-" sale de que la gravedad siempre apunta para abajo), necesitamos solo la componente radial del peso, como el peso siempre apunta hacia abajo, la componente radial siempre apunta hacia el centro, por la relación con el angulo que ya habíamos establecido antes, la componente radial es -mgSen(T).
La componente angular del peso no se calcula por que es irrelevante para este problema. Aquí no hay Px ni Py, ya que las coordenadas "x" y "y" tomadas como en los problemas de plano inclinado (con respecto al objeto) están siempre cambiando de dirección y la fuerza normal, que es la parte importante de este problema, va siempre en dirección radial.
Cualquier duda, puedes preguntar
¿Entonces qué es lo más correcto? Puesto que el problema trata unicamente desde el momento en que el objeto comienza a moverse y hasta que se desprende de la superficie hemisferica, el movimiento que hace es circular, así que las coordenadas más correctas son las polares (radio y angulo), y escogemos como el origen al centro de la hemisfera (si fuera una esfera completa) y el angulo corresponde al angulo que hace la posición del objeto con respecto de la superficie donde esta el hemisferio, a la energía no le importa las coordenadas que uses, así que usamos las mismas energías potencial, cinética y total; ahora no tenemos que dividir la fuerza normal en componentes, ya que la fuerza normal siempre va en dirección radial, y la fuerza centrípeta ya la tenemos, como usamos coordenadas polares la fuerza centrípeta esta en función de R y no de (x+y)^1/2, entonces solo falta encontrar la componente del peso en dirección radial, el peso siempre apunta hacia abajo, así que en coordenadas cartesianas el peso es -mg en dirección de "y" (el "-" sale de que la gravedad siempre apunta para abajo), necesitamos solo la componente radial del peso, como el peso siempre apunta hacia abajo, la componente radial siempre apunta hacia el centro, por la relación con el angulo que ya habíamos establecido antes, la componente radial es -mgSen(T).
La componente angular del peso no se calcula por que es irrelevante para este problema. Aquí no hay Px ni Py, ya que las coordenadas "x" y "y" tomadas como en los problemas de plano inclinado (con respecto al objeto) están siempre cambiando de dirección y la fuerza normal, que es la parte importante de este problema, va siempre en dirección radial.
Cualquier duda, puedes preguntar

Hola,
Entonces es este ángulo al que te refieres ,no?: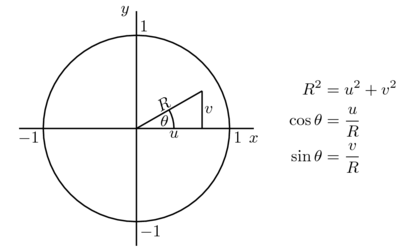
El radio es la fuerza centrípeta que en este caso al ser coodenadas polares coincide con la fuerza normal y también con la dirección radial del peso ... por tanto:
sen(T)= P ("v"del dibujo)/m*g ----> P =sen(T) * m*g
Podrías indicarme si lo siguiente es correcto?
Fuerza centrípeta=masa * aceleración normal ---> m*V^2/r=sen(T)*m*g y me queda :
V^2 = g*sen(T)*R . Pero si quisiera obtener el ángulo desde el punto 1 hasta donde se desprende el objeto : P = cos(T) *m*g y por tanto V^2= g*cos(T)*R.
Has explicado que la enegía se conserva...entonces Ep en 1 = Ep en pto 2 + Ec y considerando el (T) del dibujo) me queda: m*g*R= m*g*R*sen(T) + 1/2 m*v^2
Ahora sustituyo v^2 =R*g*sen(T)
Gracias.
Entonces es este ángulo al que te refieres ,no?:

El radio es la fuerza centrípeta que en este caso al ser coodenadas polares coincide con la fuerza normal y también con la dirección radial del peso ... por tanto:
sen(T)= P ("v"del dibujo)/m*g ----> P =sen(T) * m*g
Podrías indicarme si lo siguiente es correcto?
Fuerza centrípeta=masa * aceleración normal ---> m*V^2/r=sen(T)*m*g y me queda :
V^2 = g*sen(T)*R . Pero si quisiera obtener el ángulo desde el punto 1 hasta donde se desprende el objeto : P = cos(T) *m*g y por tanto V^2= g*cos(T)*R.
Has explicado que la enegía se conserva...entonces Ep en 1 = Ep en pto 2 + Ec y considerando el (T) del dibujo) me queda: m*g*R= m*g*R*sen(T) + 1/2 m*v^2
Ahora sustituyo v^2 =R*g*sen(T)
Gracias.

Si, es correcto, me refiero a ese angulo.
La obtención que hace del peso en dirección radial es correcta, excepto por el hecho de que la componente radial del peso siempre apunta hacia el centro, por lo que debe tener signo negativo, Pr=-Sen(T)*m*g, si apuntara hacia el exterior seria positivo, pero apunta hacia el centro, así que es negativo, y recuerda también que es la componente radial del peso, no es el peso completo, ya que es solo la componente radial la que entra en la fuerza normal.
Ahí te has equivocado, la fuerza centrípeta no es masa por aceleración normal, es masa por aceleración angular, como la aceleración angular es -v^2/r, ya que también va en dirección hacia el centro (es la que mantiene al objeto en movimiento circular), la fuerza centrípeta es -mv^2/r, así que todas las igualdades que obtuviste a partir de "masa*aceleración normal" son incorrectas.
Como podras ver, al final, cuando sustituyes v^2=R*g*sen(T), obtienes
m*g*R=m*g*R*Sen(T)+(1/2)*m*g*R*Sen(T)=(3/2)*m*g*R*Sen(T)
Lo cual evidentemente no es cierto, ya que tu v^2 es incorrecto, lo correcto es obtener v^2 a partir de
m*g*R=m*g*R*Sen(T)+(1/2)m*v^2 => mv^2=2mgR(1-Sen(T))
Y eso lo sustituyes en la fuerza centrípeta para obtener una expresión para la fuerza normal que solo depende de T, y así obtener el angulo en el cual el objeto se despega del hemisferio, que corresponde a Fuerza Normal=0.
Si te queda alguna duda, puedes preguntar.
La obtención que hace del peso en dirección radial es correcta, excepto por el hecho de que la componente radial del peso siempre apunta hacia el centro, por lo que debe tener signo negativo, Pr=-Sen(T)*m*g, si apuntara hacia el exterior seria positivo, pero apunta hacia el centro, así que es negativo, y recuerda también que es la componente radial del peso, no es el peso completo, ya que es solo la componente radial la que entra en la fuerza normal.
Ahí te has equivocado, la fuerza centrípeta no es masa por aceleración normal, es masa por aceleración angular, como la aceleración angular es -v^2/r, ya que también va en dirección hacia el centro (es la que mantiene al objeto en movimiento circular), la fuerza centrípeta es -mv^2/r, así que todas las igualdades que obtuviste a partir de "masa*aceleración normal" son incorrectas.
Como podras ver, al final, cuando sustituyes v^2=R*g*sen(T), obtienes
m*g*R=m*g*R*Sen(T)+(1/2)*m*g*R*Sen(T)=(3/2)*m*g*R*Sen(T)
Lo cual evidentemente no es cierto, ya que tu v^2 es incorrecto, lo correcto es obtener v^2 a partir de
m*g*R=m*g*R*Sen(T)+(1/2)m*v^2 => mv^2=2mgR(1-Sen(T))
Y eso lo sustituyes en la fuerza centrípeta para obtener una expresión para la fuerza normal que solo depende de T, y así obtener el angulo en el cual el objeto se despega del hemisferio, que corresponde a Fuerza Normal=0.
Si te queda alguna duda, puedes preguntar.

Hola,
Voy a volver a hacer el ejercicio de esta forma porque me da la misma solución ... ¿me podrías indicar si está correcto y no me da de casualidad?
Si , antes me he equivocado al decir que Fcp= masa * aceleración Normal. Pero según la duda que pregunté con titulo"Fuerza centrípeta" (Fcp)en la cual explicaste los signos muy bien:
Fcp= Fuerza Normal * Fuerza Peso ---> -Fcp= +F N * - F peso; que sería lo mismo que escribir: Fcp= P - FN ---> FN=o y queda : m* V^2/r= m*g*sen(T)
Tras simplificar quito las m y luego despejo V: V^2= R*g*sen(T)
Ahora lo sustituyo en: m*g*R=m*g*R*sen(T) + 1/2 m *g*sen(T)
simplifico y quito las m: g*R*sen(T)/2 = g*R-g*R*sen(T)
que es lo mismo que : g*R*sen(T)/2= g*R (1-sen(T))
simplifico y se va g*R: sen(T)/2=1-sen(T)
2-2sen(T)=senT) ----> 2=3sen(T) ----> sen(T) = 2/3
Gracias.
Voy a volver a hacer el ejercicio de esta forma porque me da la misma solución ... ¿me podrías indicar si está correcto y no me da de casualidad?
Si , antes me he equivocado al decir que Fcp= masa * aceleración Normal. Pero según la duda que pregunté con titulo"Fuerza centrípeta" (Fcp)en la cual explicaste los signos muy bien:
Fcp= Fuerza Normal * Fuerza Peso ---> -Fcp= +F N * - F peso; que sería lo mismo que escribir: Fcp= P - FN ---> FN=o y queda : m* V^2/r= m*g*sen(T)
Tras simplificar quito las m y luego despejo V: V^2= R*g*sen(T)
Ahora lo sustituyo en: m*g*R=m*g*R*sen(T) + 1/2 m *g*sen(T)
simplifico y quito las m: g*R*sen(T)/2 = g*R-g*R*sen(T)
que es lo mismo que : g*R*sen(T)/2= g*R (1-sen(T))
simplifico y se va g*R: sen(T)/2=1-sen(T)
2-2sen(T)=senT) ----> 2=3sen(T) ----> sen(T) = 2/3
Gracias.

Ok, ahora te ha salido muy bien, y es un excelente camino alterno a la solución, el único detalle, tal vez error de dedo, donde dices
"...Ahora los sustituyo en: m*g*R=m*g*R*sen(T) + 1/2 m *g*sen(T)..."
Te falto colocar la R en el termino que sale de la energia cinetica, deberia ser:
m*g*R=m*g*R*sen(T) + 1/2 m*g*[R]*sen(T), puse entre "[]" el termino que olvidaste
Y tambien donde pones "Fcp= Fuerza Normal * Fuerza Peso", supongo que quisiste poner "Fcp= Fuerza Normal + Fuerza Peso"
Todo lo demás es correcto, por eso supongo que habrás olvidado escribir ese R. Pero todo te ha quedado muy bien y has llegado a la respuesta.
Supongo que ahora no tendrás dudas, pero si las tienes no olvides preguntar.
"...Ahora los sustituyo en: m*g*R=m*g*R*sen(T) + 1/2 m *g*sen(T)..."
Te falto colocar la R en el termino que sale de la energia cinetica, deberia ser:
m*g*R=m*g*R*sen(T) + 1/2 m*g*[R]*sen(T), puse entre "[]" el termino que olvidaste
Y tambien donde pones "Fcp= Fuerza Normal * Fuerza Peso", supongo que quisiste poner "Fcp= Fuerza Normal + Fuerza Peso"
Todo lo demás es correcto, por eso supongo que habrás olvidado escribir ese R. Pero todo te ha quedado muy bien y has llegado a la respuesta.
Supongo que ahora no tendrás dudas, pero si las tienes no olvides preguntar.

Si, al volver a escribir me olvidé de "R" en la fórmula de la energía cinética. También quise escribir : Fcp= FN +F peso.
De nuevo, gracias. Ahora me ha quedado claro el ejercicio.
De nuevo, gracias. Ahora me ha quedado claro el ejercicio.
- Compartir respuesta
- Anónimo
ahora mismo
