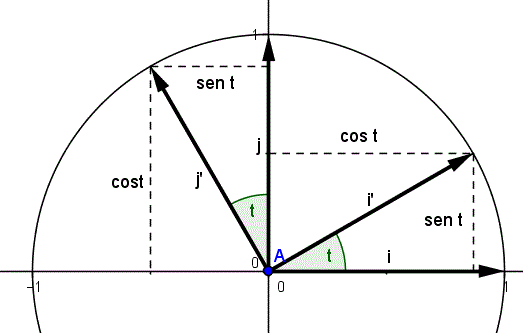
Calcular matriz de cambio de coordenadas?
Tengo este otro ejercicio en donde me piden calcular una matriz de cambio de base de un sistema coordenado. Explicame paso a paso como se resuelve y que temas hay que saber para resolver este tipo de ejercicios.
Aquí esta el enlace:
1 respuesta
a)
El vector i es (1,0). Si lo giramos un angulo t tendremos el vector (cost, sent)
El vector j es (0,1), al girarlo un ángulo t queda el vector (-sent, cost)
b)
La matriz del cambio de coordenadas o (de cambio de base) se forma con la coordenadas de la base original en función de las nuevas puestas por columnas
La base original es {(1,0), (0,1)}
La nueva es {(cost, sent), (-sent,cost)}
a·cost - b·sent = 1
a·sent + b·cost = 0
Multiplicamos la segunda por sent/cost
a·sen^2(t) /cost + bsent = 0
La sumamos con la primera
a·cost+a·sen^2(t) / cost = 1
a·cos^2(t) +a·sen^2(t) = cost
a[cos^2(t)+sen^2(t)] = cost
a=cost
cost·sent + b cost= 0
b= -sent
Luego las coordenadas de (1,0) en la base nueva son (cost, - sent)
Y haciendo lo mismo con (0,1) salen (sent, cost)
Y poniéndolas por columnas nos da la matriz
Cost sent -Sent cost
Y eso es todo.
no entiendo de donde sacas esas nuevas coordenadas del literal a), lo siento, podrías explicarme no se, con algo gráfico. como las calculaste
Es muy sencillo, no pensé que hubiera problema. Aquí tienes el gráfico con los vectores i, j y sus rotaciones i' y j' tras rotar un ángulo t.
Se ve que el vector i se transforma en i'= (cost, sent) y el vector j en j'=(-sent, cost)
