Estadística matemática con aplicaciones k

4.16)

a)
La función de distribución en un punto x es la integral definida de la función de densidad entre -infinito y ese punto. Como hasta cero la función es nula podemos poner cero como límite inferior.
F(y) = $(c(2-t))dt entre 0 e y =
c[2t-(t^2)/2] entre 0 e y =
c[2y-(y^2)/2]
Y las condiciones de una función de distribución son:

1) Que valga 0 en el -infinito. La cumple

2) Que valga 1 en el infinito.

Donde la función de densidad sea cero la de distribución no puede aumentar. En nuestro caso, f es nula a partir de 2, luego:
F(2) = 1 ==> c [2·2-(2^2)/2] = 1 ==> c(4-2) = 1 ==> c = 1/2

b)
F(y) = 0 si y € (-oo, 0)
y - (y^2)/4 si y € [0, 2]
1 si y € (2, +oo)

c) Estas son las funciones:

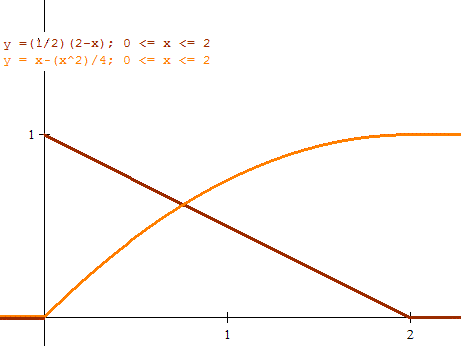
En marrón más oscuro la función de densidad, más claro la de distribución.

d) d) P(y€[1, 2]) = F(2) - F(1) = 1 - [1 -(1^2)/4] = 1-(1-1/4) = 1-3/4 = 1/4

e) Dividimos el triangulo formado por función de densidad (marrón oscuro) y los ejes
En cuatro iguales al que se forma desde el punto 1 al 2. Luego el triangulo entre 1 y 2 tiene por área 1/4. Esa área es precisamente la probabilidad de que la función valga entre 1 y 2.

Y eso es todo.