Transformación de variables aleatorias

A)

La integral entre -oo y +oo de la función de densidad debe valer 1. Como la función de densidad vale cero fuera del intervalo (-1, 1) es dentro de ese intervalo donde la integral debe valer 1. La integral coincide con el área de la figura formada entre la gráfica de la función y el eje X. Es un triángulo de base 2. Por la fórmula del área del triángulo tenemos:

2b/2 = 1

b=1

Los subintervalos serán:

[-1, -1/2),

[-1/2, 0)

[0, 1/2)

[1/2, 1)

Los puntos medios y sus probabilidades son:

P(-3/4) = (1/2)(1/2) /2 = 1/8

P(-1/4) = (1/2)-(1/8) = 3/8

P(1/4) = P(-1/4) = 3/8

P(3/4) = P(-3/4) = 1/8

B)

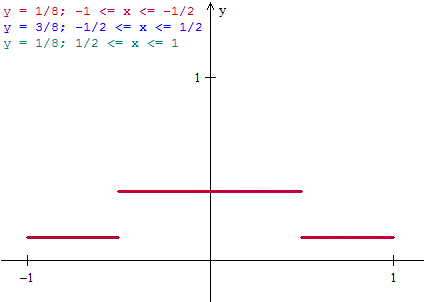
C)

La media de Y es:

E(Y) = -(3/4))(1/8) - (1/4)(3/8) + (1/4)(3/8) + (3/4)(1/8) = 0

y la varianza de Y es:

V(Y) = (3/4)^2·(1/8) + (1/4)^2 (3/8) + (1/4)^2·(3/8) + (3/4)(1/8) =

2[(9/16)(1/8) + (1/16)(3/8)] = 2(9/128 + 3/128) = 24/128 = 3/16

Para calcular la media y varianza de X establezcamos la función de densidad

f(x) = 0 si x < -1

x+1 si -1 <= x <= 0

1-x si 0 <= x <= 1

0 si x > 1

La media de X es:

[$(x+1)xdx entre -1 y 0] + [$(1-x)xdx entre 0 y 1] =

[(x^3)/3 + (x^2)/2 entre -1 y 0] + [(x^2)/2 - (x^3)/3 entre 0y 1] =

= 1/3 -1/2 +1/2 -1/3 = 0

L varianza de X es:

[$(x+1)x^2dx entre -1 y 0] + [$(1-x)x^2dx entre 0 y 1] =

[(x^4)/4 + (x^3)/3 entre -1 y 0] + [(x^3)/3 - (x^4)/4 entre 0y 1] =

-1/4 + 1/3 +1/3 -1/4 = (-3+4+4-3)/12 = 2/12 = 1/6

Las medias coinciden, las varianzas no. Traducido a decimal para poder compararlo mejor es:

V(Y) = 0,1875

V(X) = 0,1666...

Y eso es todo.