En este ya veo que la gráfica puede ayudar bastante.
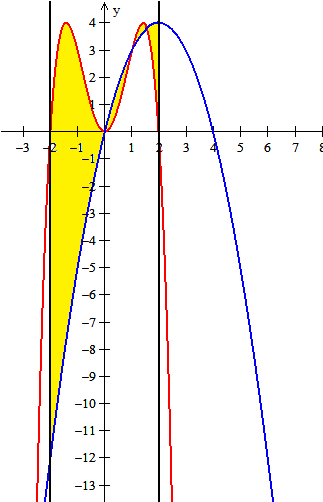
Se ve claramente que hay cuatro zonas donde cambia la función mayor por la menor.
Debemos calcular esos puntos que son donde loas dos funciones valen igual, o bien donde su diferencia es cero
-x^4 + 4x^2 + x^2 - 4x =0
-x^4 + 5x^2 - 4x = 0
Vale se ve perfectamente que x= 0 es una. Dividimos entre x y de paso cambiamos el signo
x^3 - 5x + 4 = 0
Menos mal que se ve fácilmente que x=1 es otra respuesta
Dividimos por x-1
1 0 -5 4
1 1 1 -4
-------------
1 1 -4 |0 Y las otras dos las calculamos resolviendo la ecuación
$$\begin{align}&x=\frac{-1\pm \sqrt{1+16}}{2} =\\ &\\ &x=\frac{-1\pm \sqrt{17}}{2}\end{align}$$La del signo - es -2.56... es la de la izquierda que falta un poco para verla, no la necesitamos ya que esta a la izquierda del intervalo
La de signo más vale aproximadamente 1.56, es el punto de más a la derecha donde se cortan. Para abreviar la voy a llamar r
Luego tendremos que hacer la integral indefinida de la diferencia de las funciones y evaluarla en estos intervalos
[-2, 0], [0,1], [1, r] y [r, 2]
Y sumar los valores absolutos que obtengamos.
La integral es la de la diferencia que ya usamos antes, pero esta vez hago la resta al revés para que que queden mejor los signos
g(x)-f(x) = x^4 - 5x^2 + 4x
y la integral indefinida es
(1/5)x^5 -(5/3)x^3 +2x^2
Y ya hemos hecho una tarea bastante completa, ahora haré esas evaluaciones con el ordenador que ya me empieza a arder la cabeza.
En [-2,0] es -224/15
en [0,1] es 8/15
en [1,r] es [138-34sqrt(17)]/15 = -0.1456060847
en [r,2] es (34sqrt(17)-130)/15 = 0.6790394181
Para sumarlos tener en cuenta que en el tercero debemos cambiar el signo de los dos términos.
Área total = [224 + 8 - 138 -130 + 68sqrt(17)] / 15 =
[68sqrt(17) - 36] / 15 u^2
Aproximadamente
16.29141217 u^2
Y eso es todo.

