Explicación sobre circulo osculador ejercicio 20

Eso es más bien un tema de teoría, me vendría bien saber el libro.

El circulo osculador es el circulo que mejor se adapta a una curva en un punto. Asi como todos tenemos la idea de la recta tangente en un punto, hay una circunferencia que es la que más se asemeja a una curva en un punto. Se calcula porque esta en la normal a la curva y su radio es 1/K donde K es la curvatura en ese punto. Ahora no me acuerdo de mucho más, sobre todo la parte de cómo se calcula hacia que lado de la tangente se sitúa, pero ya lo miraré cuando haga el ejercicio.

Pues para resolverlo me gustaría saber si os han dado alguna fórmula directa para la curvatura de funciones de una variable. Y la parte de comparar no puedo hacerla si no resuelvo los ejercicios 16 y 19, pero eso tendrías que mandármelo en otras dos preguntas.

no valeroasm no me han dado ninguna formula, solo para funciones de varias variables. igual te voy a enviar el ejercicio 16 y 19 individualmente para que mires y puedas con este.es que no entiendo mucho ni me alcanzo a imaginar como es un circulo osculador. ayudame con eso en este punto en particular.

En la página 494-495 nos dan la fórmula para la curvatura de una función y = f(x)

$$K(x) =\frac{f''(x)}{\sqrt{\left[1+(f'(x))^2\right]^3}}$$

Y en la página 501 te da la fórmula para calcular el centro del círculo osculador o circunferencia osculatriz que sería más exacto. Y en esa misma página hay un ejemplo, vamos a usarlo.

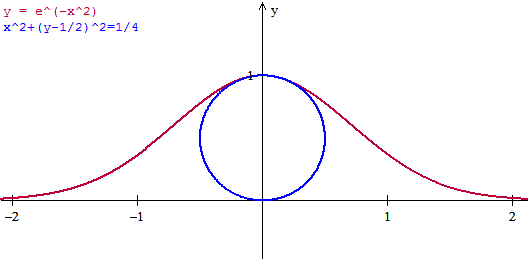
La función y = e^(-x^2) en el punto (0,1)

$$\begin{align}&f'(x) = -2xe^{-x^2}\\ &\\ &f''(x) = -2e^{-x^2}+4x^2e^{-x^2}=e^{-x^2}(4x^2-2)\\ &\\ &K(x) =\frac{f''(x)}{\sqrt{\left[1+(f'(x))^2\right]^3}}=\\ &\\ &\\ &\frac{e^{-x^2}(4x^2-2)}{\sqrt{(1+4x^2e^{-x^2})^3}}\\ &\\ &\\ &K(0) =\frac{-2}{1}=-2\\ &\\ &\\ &\text{Y el centro será}\\ &\left(x(0)- \frac{y'(0)}{K(0)||f'(0)||},y(0)+\frac{x'(0)}{K(0)||f'(0)||}  \right)=\\ &\\ &donde \quad x(t)=t\;;\quad y(t)=e^{-t^2}\;;\quad f'(t)=(1,-2te^{-t^2})\\ &\\ &x(0)=0\;;\quad y(0)=1\;\quad ||f'(0)||=\sqrt{1^2+0^2}=1\\ &\\ &\\ &=\left(0-\frac{0}{-2·1},1+\frac{1}{-2·1}  \right)=\left(0,\frac 12\right)\\ &\\ &\text{y el radio es el inverso de la curvatura}\\ &R=\frac 1{|-2|}=\frac 12\\ &\\ &\text{Luego la circunferencia osculatriz es}\\ &\\ &(x-x_c)^2+(y-y_c)^2 = R^2\\ &\\ &x^2+\left(y-\frac 12\right)^2= \frac 14\end{align}$$

Está bien y es perfecta para que veas lo que es la circunferencia osculatriz como la circunferencia que mejor se adapta la curva en un punto.

Es una circunferencia que debe pasar por el punto (0,1) y tener las mismas derivadas primera y segunda que la curva.

Y eso es todo, espero que te sirva y lo hayas entendido. Hoy no hice mucho trabajo, estoy saturado con estos problemas que siempre me gustaron poco y no solo estoy recibiendo los tuyos sino otros.