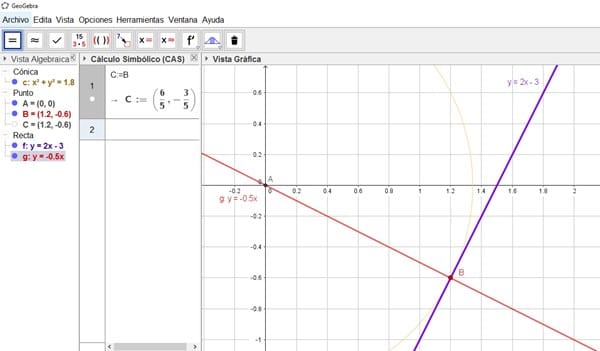
Punto cercano al origen de y=2x-3
Halle el punto de la recta más cercano al origen de la pendiente y=2x-3
3 Respuestas
Adjunto una solución gráfica para complementar la respuesta analítica de Valero
La distancia de un punto a una recta se mide a través de la perpendicular a la recta que pasa por el punto.
Si nos dan la recta en la forma
y=mx+b tenemos que la pendiente de la recta es m.
Luego en y=2x-3 la pendiente es 2
Una propiedad que cumplen las pendientes de dos rectas perpendiculares en el plano es que el producto de las pendientes es -1.
luego llamando m a la pendinete de la perpendicular tendremos
2m = -1
m = -1/2
Luego la perpendicular será
y =-(1/2)x + b
y como pasa por (0,0)
0 = 0 +b
b=0
luego la perpendicular es
y = -x/2
Y ahora hallamos la intersección de las dos rectas
y=-x/2
y = 2x-3
igualando
-x/2 = 2x - 3
-x = 4x - 6
5x = 6
x=6/5
y ahora calculamos y
y=-(6/5)/2 = -6/10 = -3/5
Luego el punto es (6/5, -3/5)
·
Y eso es todo, espero que te sirva y lo hayas entendido.
Estoy pensando yo ahora si este era un ejercicio de máximos y mínimos, como no has dicho nada yo lo he tomado por ejercicio de geometria euclidea.
Si fuera de máximos y mínimo mándalo en otra pregunta distinta que aquí ya se ha trabajado bastante.
La distancia de un punto (x, y) al origen es:
$$\begin{align}&d=\sqrt{x^2+y^2}\\&\\&\text{Los puntos son de la recta }\\&y=2x-3\\&\text{luego la distancia es una función solo de x}\\&\\&d(x) = \sqrt{x^2+(2x-3)^2}\\&\\&\text{derivamos e igualamos a 0}\\&\\&d'(x)= \frac{2x+2(2x-3)·2}{2 \sqrt{x^2+(2x-3)^2}}=0\implies\\&\\&2x+8x-12=0\\&\\&10x = 12\\&\\&x=\frac 65\\&\\&y=2· \frac 65-3= \frac{12}{5}-3=-\frac 35\\&\\&\\&\text{el punto es: } \left(\frac 65,-\frac 35 \right)\end{align}$$