Dada una empresa donde sus costos fijos son de $75 y sus costos variables son de $1500 f(x)=11x^2+124x+7
1.- Calcula el costo promedio.
2.- ¿Cuál es el costo promedio de producción de la empresa en el límite, cuando el número de miles de productos x tiende a infinito? Y ¿Qué sucede con los costos fijos de producción promedio cuando “x” tiende a infinito?
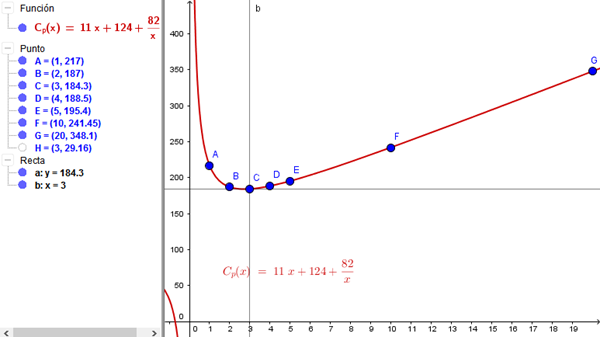
3.- Para analizar el comportamiento de la función de costo promedio, debe realizar una tabla de pares ordenados y realizar la gráfica de la función de costo promedio.
4.- ¿En x= 0, la función de costo promedio es continua o discontinua? ¿Por qué?
5.- A partir de la gráfica realizada, ¿cuántos miles de artículos de “x” tiene que producir la empresa para minimizar el costo promedio?
1 Respuesta
·
·
¡Hola Karla!
El enunciado no está bien. Los costos variables serán una función de x, puedo suponer que sean
f(x)=11x^2+124x+7
¿entonces que pinta $1500?
O bien es un dato que sobra o bien son los auténticos costos fijos en lugar de los $75.
No pueden coexistir los tres datos, sobra alguno.
Revisa el enunciado y espero la aclaración.
Hola Valero, muchas gracias por responderme, efectivamente sobran los 1500. Solo hay que tomar como costo fijo los 75.
Gracias = )
1) Primero calculamos el costo total
CT(x) = CV(x) + CF
CT(x) = 11x^2 + 124x + 7 + 75
CT(x) = 11x^2 + 124x + 82
Y el costo propmedio es el costo total dividido por x
Cp(x) = (11x^2 + 124x + 82) / x
Cp(x) = 11x + 124 + (82/x)
·
2)
$$\begin{align}&\lim_{x\to\infty}C_p(x)=\lim_{x\to\infty}\left(11x+124+\frac{82}{x}\right)=\\&\\&\infty+124+0=\infty\\&\\&\text{El costo promedio de producción es infinito}\\&\\&\\&\text{Los costos fijos promedio en el infinito son}\\&\\&\lim_{x\to\infty}\frac{75}{x}=0\end{align}$$3)
La tabla del costo promedio sería:
Cp(x) = 11x + 124 + (82/x)
0 ---> infinito
1 ---> 217
2 ---> 187
3 ---> 184.3
4 ---> 188.5
5 ---> 195.4
10 ---> 241.45
20 ---> 348.1
Esta es la gráfica:
En x=0 la función es discontinua porque el límite es infinito, para ser continua debería ser un límite finito que coincidiese con el valor de la función. Y el valor de la función no está definido porque no se puede dividir por 0.
·
5) La gráfica parece que tiene el mínimo en x=3 (más o menos)
Luego haría falta vender 3 miles de artículos.
No obstante se puede calcular exacto
$$\begin{align}&C_p'(x)=11-\frac{82}{x^2}=0\\&\\&x^2=\frac{82}{11}\\&\\&x= 2.73\end{align}$$Era muy difícil ver el mínimo y los ojos se te iban al 3.
:
:
