Determinar valores críticos de una función
Considera la función, . Determina lo siguiente:
f(x)= (2x-1)^2(9-x)
- La derivada de la función, lo más simplificada posible.
- Los valores críticos de la función.
- Si los valores críticos son máximos o mínimos.
- Los intervalos de crecimiento y de decrecimiento de la función.
Tercera parte:
Usted ha determinado que el comportamiento de sus utilidades, en función del precio de su producto, está dado por la expresión, U(p)=400(15-p)(p-2), donde la utilidad está dada en cientos de pesos y el precio está limitado por el intervalo . Mediante derivación, determina el precio al que la utilidad es máxima, y calcule ese valor óptimo.
1 Respuesta
·
·
¡Hola Beatriz!
En toda pregunta que tenga relación con las matemáticas no debe faltar la categoría de Matemáticas, porque es la primera que miramos, y si tenemos mucho trabajo en ella ya no miramos otras categorías.
Son dos ejercicios independientes hará solo el primero, si quieres el segundo mándalo en una pregunta nueva.
Lo de lo más simplificada posible a lo mejor no te gusta. Yo la voy a hacer lo más simplificada posible para calcular fácilmente las raíces, porque eso es lo que me van a pedir después. Si la primera derivada no hiciera falta para nada y lo que fuera importante fuera la segunda, entonces la primera la simplificaría de otra forma
$$\begin{align}&f(x)=(2x-1)^2(9-x)\\&\\&f'(x) = 2(2x-1)·2·(9-x)+(2x-1)^2(-1) =\\&\\&(2x-1)(36-4x-2x +1) = (2x-1)(37-6x)\\&\\&\text{esa es la simplificación mejor para lo que viene}\\&\\&\\&\\&\text{2) Los valores críticos son los que }f'(x)=0\\&\\&(2x-1)(37-6x)=0\\&2x-1=0 \implies 2x=1 \implies x=\frac 12\\&37-6x=0\implies6x=37\implies x=\frac{37}{6}\\&\\&\text{3) La derivada segunda es}\\&f''(x)=2(37-6x)+(2x-1)·(-6)=\\&2(37-6x-6x+3)=2(40-12x)\\&\\&f''\left(\frac 12\right)=2(40-6)=72\implies mínimo\\&\\&f''\left( \frac {37}6\right)=2(40-74)=-68\implies máximo\\&\\&\text{4) Antes de un mínimo decrece, luego crece}\\&\text{Antes de un máximo crece y luego decrece, luego}\\&\\&\left(-\infty,\frac 12\right) decreciente\\&\\&\left( \frac 12,\frac{37}{6}\right) creciente\\&\\&\left( \frac{37}{6},\infty\right) decreciente\end{align}$$Esta es la gráfica que confirma los resultados:
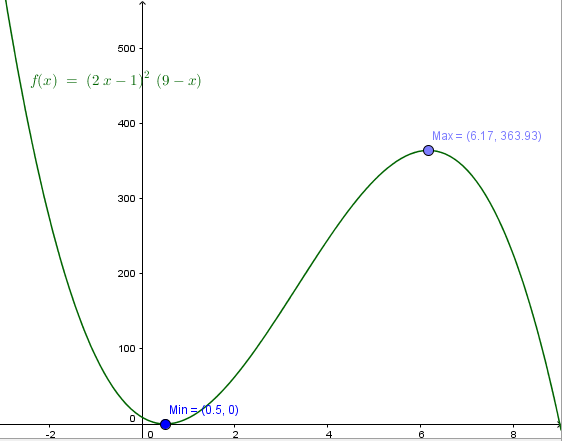
Y eso es todo, espero que te sirvay lo hayas entendido. Si no es así pregúntame. Y si ya está bien, no olvides valorar la respuesta.
Saludos.
:
.
