Plantee el modelo que optimiza la capacidad del canalón.

·

·

¡Hola Jhon!

Haré el primero si puedo que ya es suficiente trabajo, el otro tendrás que mandarlo en otra pregunta.

Las parábolas serán curvas de la forma

y=ax^2  con a>0

Debemos calcular el punto xo tal que la longitud de la parábola entre -xo y xo sea 30 para luego calcular el área mediante integrales y optimizar esa función del área.

La integral de la longitud es complicadísima (por no decir lo que pienso) mediante cambios de variable específicos para raíces cuadradas o trigonométricos, así que usaré cambios hiperbólicos.

$$\begin{align}&L=\int_a^b \sqrt{1+\left(f'(x)\right)^2}\;dx\\&\\&f(x)= ax^2\\&f'(x) = 2ax\\&\\&\text{Como la parábola es simetrica tomo la mitad de la longitud}\\&\text{y la integral entre 0 y }x_0\\&\\&\int _0^{x_0} \sqrt{1+4a^2x^2}dx=15\\&\\&x=\frac{sh\,t}{2a}\\&\\&dx=\frac{ch\,t}{2a}dt\\&\\&x=0\implies t=0\\&x=x_0\implies t= argsh(2ax_0)\\&\\&\int_0^{argsh(2ax_0)}\sqrt{1+sh^2t}·\frac{ch\,t}{2a}dt= \\&\\&\frac 1{2a}\int_0^{argsh(2ax_0)}ch^2tdt= \\&\\&\frac 1{2a}\int_0^{argsh(2ax_0)}\left(\frac 12+\frac {ch\,2t}{2}  \right)dt=\\&\\&\frac 1{2a}\left[\frac t2+\frac{sh \,2t}{4}  \right]_0^{argsh(2ax_0)}=\\&\\&\frac 1{2a}\left(\frac{argsh(2ax_0)}{2} +\frac{sh(2argsh(2ax_0))}{4} \right)=\\&\\&\frac 1{2a}\left(\frac{argsh(2ax_0)}{2} +\frac{2sh(argsh(2ax_0))·ch(argsh(2ax_0))}{4} \right)=\\&\\&\frac 1{2a}\left(\frac{argsh(2ax_0)}{2} +\frac{sh(argsh(2ax_0))·ch(argsh(2ax_0))}{2} \right)=\\&\\&\frac {1}{4a}\left(argsh(2ax_0)+2ax_0 \sqrt{1+4a^2x_0^2}\right)=\\&\\&\frac{1}{4a} \left(ln\left(2ax_0+\sqrt{1+4a^2x_0^2}\right)+2ax_0 \sqrt{1+4a^2x_0^2}  \right)=15\\&\end{align}$$

Que yo sepa todavía nadie ha sido capaza de despejar x_0 en esa ecuación.  Dejémosla como está

Por otra parte el área, o mejor la mitad del área que tendrá el canalón será

$$\begin{align}&\frac A2=\int_0^{x_0}(ax_0^2-ax^2)dx=\\&\\&\left[ax_0^2\,x-\frac{ax^3}{3}  \right]_0^{x_0}=\frac{2ax_0^3}{3}\\&\\&\text{Luego tenemos que maximizar la función}\\&\\&A(a,x_0)=\frac 43ax_0^3\\&\\&\text{ligada a la ecuación}\\&\\&\varphi(a,x_0)=\frac{1}{4a} \left(ln\left(2ax_0+\sqrt{1+4a^2x_0^2}\right)+2ax_0 \sqrt{1+4a^2x_0^2}  \right)-15=0\\&\\&\text{usaremos un multiplicador de Lagrange } \lambda\\&\\&\frac{\partial A}{\partial a}+\lambda·\frac{\partial \varphi}{\partial a}=0\\&\\&\text{me vas a permitir que la derivada la haga con ordenador}\\&\\&\end{align}$$

Y visto lo visto voy a dejarlo, ya sabía desde el principio que no podría pero ahora estoy seguro.

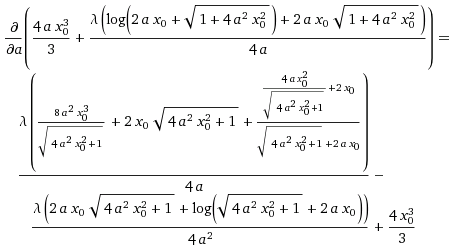
Como puedes ver quedarán siempre ecuaciones com mezcla de logaritmos con raíces cuadradas que son irresolubles.

Solo con métodos numéricos se podría dar una solución aproximada, pero tampoco será fácil.

¿Era esto de verdad un ejercicio de los estudios? Si es así cuéntame un poco el tema que estáis estudiando.

Y eso es todo.

Salu_dos.

:
:

De todas formas el ejercicio decía plantee el modelo, no decía de resolverlo. Además que yo no sé qué métodos usáis para resolverlo, con el mío desde luego lo tenéis crudo.

Entonces la terminación del planteamiento es que hay tres ecuaciones, la de esa derivada parcial que hemos calculado igualada a 0, la misma función pero con derivada parcial respecto a x_0 igualada a 0 y la ecuación phi(a, x0)=0

Con esas tres ecuaciones tendrías que despejar lambda, a y xo. Y para ese valor de a sería máxima la capacidad del canalón. Bueno, que si salieran varios valores de a habría que ver si son máximos o mínimos lo que dan. Todo bastante complicado o imposible de resolver de forma algebraica

Salu_dos.

¡Gracias! Y estás en lo cierto, básicamente mi profesor me dejó ese ejercicio para dejarlo expresado, ya que, su solución requeriría mucho trabajo, además tampoco estamos al nivel de resolver esos ejercicios. Muchas gracias por la colaboración realmente es asombroso.

Muchas gracias.

-(2)Solucione el ejercicio anterior, si ahora la forma del canalón tiene la base circular y los lados rectos.

Ahora bien este ejercicio ¿cómo lo dejaría planteado?. He intentado varias formas pero no logro encontrar la acertada.

Gracias por la colaboración.