Ecuación del círculo, dos puntos y una pendiente

·

·

¡H o l a   Llaq!

Será un punto (x,y) equidistante de los dos luego

$$\begin{align}&\sqrt{(x-3)^2+(y-5^2)}=\sqrt{(x+1)^2+(y-1)^2}\\&\\&(x-3)^2+(y-5^2)=(x+1)^2+(y-1)^2\\&\\&x^2-6x+9+y^2-10y+25=x^2+2x+1+y^2-2y+1\\&\\&-6x+9-10y+25=2x+1-2y+1\\&\\&-8x-8y+32=0\\&\\&-x-y +4 = 0\\&\\&\text{Y estará en la perpendicular a esa recta que pasa por (-1,1)}\\&\\&\text{Dada  }Ax+By + C=0\\&\text{las perpendiculares son}\\&Bx-Ay+D=0\quad ó\quad -Bx+Ay+E=0\\&\text{lo pongo siempre así para poder elegir la que haga}\\& \text{positiva a la x que es lo que me gusta.  }\\&\\&\text{Luego de }\\&3x+y+2=0\\&\text{las perpendiculares son}\\&x-3y+D=0\\&\\&\text{Como debe pasar por }(-1,1)\\&-1-3+D=0\implies D=4\\&\\&\text {es la recta}\\&x-3y+4=0\\&\\&\text{Luego tenemos el sistema}\\&-x-y +4= 0\\&x-3y+4=0\\&\\&\text{Si las sumamos}\\&-4y+8=0\\&y=2\\&\\&x=-y+4=-2+4=2\\&\\&\text{Luego el centro es }\\&(h,k)=(2,2)\\&\\&\text{Y el radio al cuadrado es}\\&R^2=(3-2)^2+(5-2)^2=1^2+3^2 = 10\\&\\&\text{Luego la ecuación es: }\quad(x-h)^2+(y-k)^2=R^2\\&\\&(x-2)^2+(y-2)^2=10\end{align}$$

Y ya que hice el dibujo de comprobación lo termino del todo y lo mando

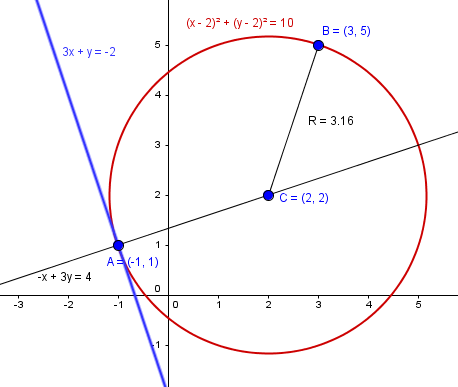
Y eso es todo, s a l u d o s.

:

: