¿Cómo resolver el siguiente ejercicio de limites principio de sustitución?
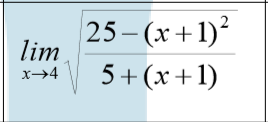como resolver el siguiente ejercicio aplicando el principio de sustitucion
Respuesta de Santiago Seeker
1
Sol hay que reemplazar el valor del límite y esperar que no se forme alguna indeterminación... en ese caso debemos levantarla usando artificios, teoremas, criterios... etc... veamos,
$$\begin{align}&\lim_{x\rightarrow4}{\sqrt{\frac{25-(x+1)^{2}}{5+(x+1)}}}=\sqrt{\frac{25-([4]+1)^{2}}{5+([4]+1)}}=\sqrt{\frac{25-(5)^{2}}{25}}=\sqrt{\frac{0}{25}}=0\end{align}$$y ese es el límite de la función.
1 respuesta más de otro experto
Respuesta de Lucas m
1
;)
Hola Fernanda!
Desde el móvil no puedo abrir el Editor de ecuaciones.
Para evaluar ese límite solo tienes que sustituir x=4
√{[25-5^2]/[5+5]}=√(0/10)=√0=0