Lo primero que hay que ver es si se cumple la premisa (que la función cambia de signo en los extremos del intervalo)
$$\begin{align}&f(0) = e^{-0}(2.1 sen(0) - 0.2 \cos(0)) = -0.2 < 0\\&f(1) = e^{-1}(2.1 sen(1) - 0.2 \cos(1)) \text{ No me voy a detener en el resultado, pero si se ve que el resultado es >0}\\&\\&\end{align}$$Visto que se cumple la premisa, entonces lo que hay que hacer ahora es definir el valor de c (punto dentro del intervalo a verificar si es 0 (lo que varía entre este método y el de bisección es justamente en el modo de calcular 'c')
Los distintos valores de 'c' se calcularán como:
$$\begin{align}&c=b - \frac{f(b) (b-a)}{f(b) - f(a)}\end{align}$$Donde 'a' y 'b' son los extremos del intervalo.
Como ahora hay que iterar hasta que f(c) < 0.005 (que es el error permitido), lo voy a hacer en una planilla Excel
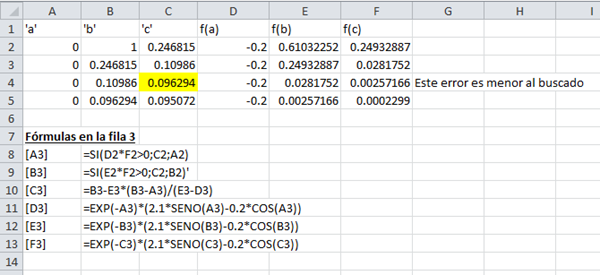
El valor buscado es el que está pintado de amarillo
Salu2


