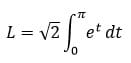Resolver la integral para la longitud de arco.
Integrales
Resolver la integral para la longitud de arco.
a)
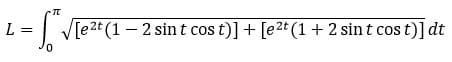
b)
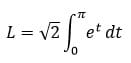
Respuesta de Lucas m
2
Integrales
Resolver la integral para la longitud de arco.
a)
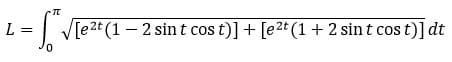
b)