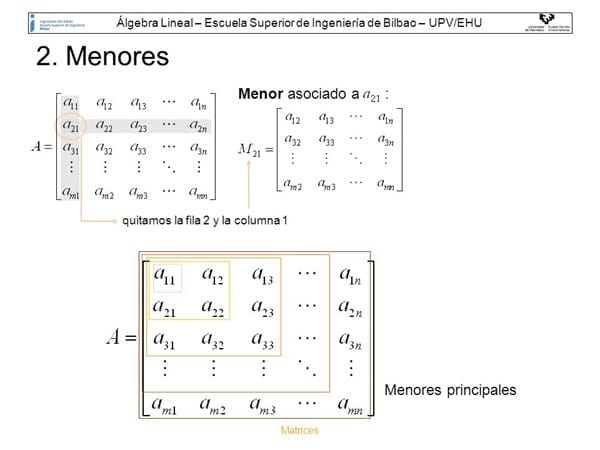
Método numérico Gauss - Seidel: Ordenar diagonal principal de cada ecuación al mayor valor
Tengo un sistema de ecuaciones 5x5 donde los valores que toma la diagonal principal no están ordenados, no se cumple la condición de que los valores de la diagonal principal sean mayores que los demás, esta es una condición inicial para aplicar correctamente el método numérico Gauss - Seidel.
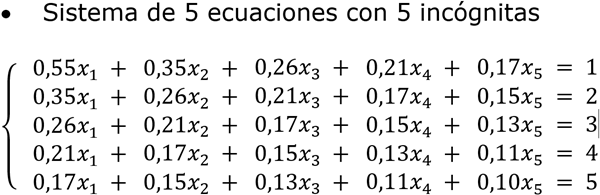
¿Se puede ordenar de alguna manera cada ecuación con sus respectivas incógnitas para que cumpla la condición de aplicación del método numérico Gauss - Seidel?
Personalmente no encontré forma de hacer esto. Agradezco de antemano cualquier ayuda / orientación.
2 respuestas
No conocía este método, voy a intentar ver si encuentro una manera de hacer que la diagonal tenga los coeficientes más grandes, pero no prometo nada
Ok buscando en internet ya entendí el método
Y encontré algo interesante y es que si la matriz es simétrica y definida positiva, converge (IMPORTANTE, solo matrices simétricas y positivas, si no es simétrica pues hay que ver si es diagonalmente dominante)
La matriz que muestras es simétrica, ahora hay que ver si es definida positiva. Ya de esto si conozco
Una matriz es definida positiva si los valores propios son todos mayores que cero, pero que fastidio hacerlo, o también si los menores principales son todos mayores que cero
¿Qué es un menor principal? Es el determinante de todas las submatrices cuadradas que hay en esa matriz, te dejo una imagen porque escrito voy a complicar más que ayudar.
y dejo el link https://slideplayer.es/slide/1032347/
Ves que la matriz la separas en matrices 1x1, 2x2, 3x3... hasta nxn (en este caso 5x5). Lo que debes hacer es comprobar que todos esos determinantes son positivos, cuando llegas al determinante 3x3 da -0.000126, determinante negativo, por lo que no es una matriz definida positiva, así que no puedes aplicar el método
Ese procedimiento manual, el primer paso ya está listo porque 0.55 es el mayor valor a 'pivotear',
El primer paso es hacer 1 el pivot (elemento A(1,1)) y esto lo consigues dividiendo toda la fila 1 entre 0.55.
Luego tienes que hacer 0 los elementos debajo del pivot
Una vez que hagas esto, debes ver de la columna 2 cual es el mayor valor (considerando de la fila 2 hacia abajo)
El mayor valor pasa a ser el pivot y lo tienes que hacer 1
Luego tienes que hacer 0 los elementos debajo del pivot (elemento A(2,2))
Sigues hasta que llegas al último elemento (en este caso A(5,5))
La ventaja de este método es que al tomar siempre el mayor pivot posible, la solución es más 'estable' (tiene que ver con métodos numéricos) y cuando termines la matriz te queda triangulada con todos los elementos de la diagonal igual a 1.
Salu2
Ojo que te respondí el método de Gauss Jordan, lo que tu precisas (Gauss Seidel) es lo que te respondió Alejandro.