La ecuación de una circunferencia es (𝑥+1)2+(𝑦−3)2=49.
La ecuación de una circunferencia es (𝑥+1)2+(𝑦−3)2=49. Justifique matemáticamente:
a) Que el punto𝐴(−1,10) esté sobre la circunferencia,
b) Que el punto𝐵(−3,2) sea interior a la circunferencia y
c) Que el punto𝐶(5,−2) es exterior a la circunferencia.
Si tenemos una circunferencia de centro C(a, b) y de radio r y tomamos cualquier punto que pertenezca a la circunferencia:
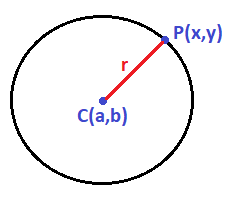
El radio siempre va a ser la distancia entre el punto P de la circunferencia y el centro C:
Te recuerdo, que la fórmula para calcula la distancia entre dos puntos es la siguiente:
Debo hallar la respuesta correcta con esta información.
a)Para que un punto pertenezca a la circunferencia, debe cumplir que si sustituyes las coordenadas en el lado izquierdo, te debe dar como resultado el lado derecho.
b)Para que pertenezca al interior de la circunferencia que al sustituir las coordenadas en el lado izquierdo debe darte un numero menor al lado derecho
c)Para que pertenezca al interior de la circunferencia que al sustituir las coordenadas en el lado izquierdo debe darte un numero menor al lado derecho
Si lo haces, fijarás que los puntos cumplen eso.
Para la última
Sabemos que la ecuación de la circunferencia es (x-a)^2+(y-b)^2=r^2
Si un punto pertenece a la circunferencia, entonces significa que debe cumplir la ecuación de arriba
Digamos que las coordenadas del punto es (x1, y1), como pertenece a la circunferencia entonces
(x1-a)^2+(y1-b)^2=r^2
Ahora usando la ecuación de la distancia entre dos puntos y usando las coordenadas del ce
$$\begin{align}&\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}=\\&\sqrt{(a-x_1)^2+(b-x_1)^2}=\sqrt{r^2}=r\end{align}$$Fijate que al usar la distancia entre dos puntos entre el centro de la circunferencia y el punto (x1,y1) nos queda (x1-a)^2+(y1-b)^2 que arriba dijimos que era r^2
