¿Cómo pasar de resolver integrales triples?

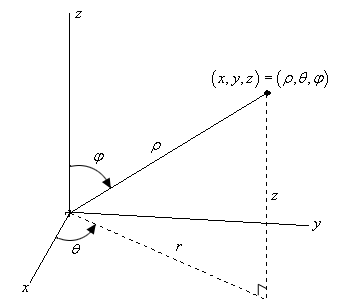
Coordenadas esféricas

$$\begin{array}{c}x = \rho \sin \varphi \cos \theta \hspace{0.25in}y = \rho \sin \varphi \sin \theta \hspace{0.25in}z = \rho \cos \varphi \\ {x^2} + {y^2} + {z^2} = {\rho ^2} \qquad \qquad 
\rho  \ge 0\hspace{0.5in}0 \le \varphi  \le \pi
\end{array}$$

En las coordenadas esféricas expresamos los puntos dada la distancia que hay de ese punto al origen que representamos con rho(la p, aunque en algunos lugares quizas la notacion cambie), la coordenada polar (theta) que nos dice el angulo que forma la proyeccion de rho en el plano XY (en la imagen creo que se ve lo que trato de decir), y luego la coordenada acimutal phi que nos dice el angulo que tiene el vector con el eje z.

En el cuadro puse cuales son los cambios.

Y además vemos que rho es siempre mayor que cero(es una distancia, no puede ser negativo).

Y phi va entre 0 y pi. ¿Por qué? Viendo la imagen veras que con theta das la vuelta completa alrededor del eje Z. Por lo que con phi solo necesitas dar media vuelta (de arriba a abajo) para alcanzar todos los puntos.

NOTA IMPORTANTE

• En un principio phi va entre 0 y pi y en un principio theta va entre 0 y 2 pi. Pero esto no es necesariamente cierto. Tienes que ver la figura que tienes, y observar si en realidad necesitas dar la vuelta completa con theta, o si es necesario dar la media vuelta completa con phi.
• Al hacer un cambio de coordenadas hay que multiplicar la integral por el jacobiano de la transformacion que es un determinante y bueno no voy a entrar en esos detalles, en el caso de las coordenadas esféricas ese factor es

  $$\begin{align}&dV = {\rho ^2}\sin \varphi \,d\rho \,d\theta \,d\varphi\end{align}$$

Asi la integral que nos queda es

$$\begin{align}&\iiint\limits_{E}{{f\left( {x,y,z} \right)\,dV}} = \int_{{\,\,\delta }}^{{\,\gamma }}{{\int_{{\,\alpha }}^{{\,\beta }}{{\int_{{\,a}}^{b}{{{\rho ^2}\sin \varphi \,\,f\left( {\rho \sin \varphi \cos \theta ,\rho \sin \varphi \sin \theta ,\rho \cos \varphi } \right)\,d\rho }}\,d\theta }}\,d\varphi }}\end{align}$$

Lo que nos dice es que en un principio tenemos una integral con respecto a x,y,z. Y luego al hacer el cambio de ccoordenadas te queda una integral triple donde en la funcion cambias los valores de x,y,z por los que puse arriba de las coordenadas esféricas y multiplicas por el jacobiano

Las coordenadas cilíndricas es básicamente las coordenadas polares pero con el eje z

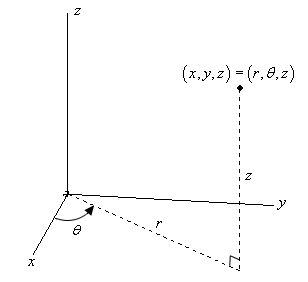
$$\begin{align}&x = r\cos \theta \hspace{0.25in}y = r\sin \theta \hspace{0.25in}z = z\end{align}$$

Expresamos los puntos solo con la distancia que hay entre el punto y el eje z(r), la altura que posee el punto(z) y luego el angulo theta  que forma la proyeccion sobre el playo XY

Vemos que la coordenada z queda igual

R es positivo porque es una distancia; y theta va entre 0 y 2pi(o entre -pi y pi, ambas son equivalentes solo que quizás en algunas ocasiones sea más fácil evaluar una u otra) por lo que da la vuelta completa.

Al igual que antes al hacer el cambio de coordenadas hay que multiplicar la integral por el jacobiano. La integral que nos queda es

$$\begin{align}&\iiint\limits_{E}{{f\left( {x,y,z} \right)\,dV}} = \int_{{\,\alpha }}^{{\,\beta }}{{\int_{{{h_1}\left( \theta  \right)}}^{{{h_2}\left( \theta  \right)}}{{\int_{{{u_1}\left( {r\cos \theta ,r\sin \theta } \right)}}^{{{u_2}\left( {r\cos \theta ,r\sin \theta } \right)}}{{r\,f\left( {r\cos \theta ,r\sin \theta ,z} \right)\,dz}}\,dr}}\,d\theta }}\end{align}$$

El jacobiano en este caso es multiplicar por r.

NOTA/

Como mencioné arriba; aquí también tienes que estar pendiente de los ángulos, y ver si en realidad es necesario que theta de la vuelta completa.

Alguna duda en concreto que tengas me dices y te respondo