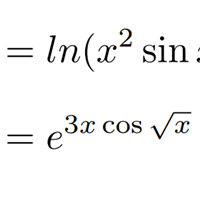Norberto Pesce

La primera, separando variables queda: x^2*lnx dx = [(y+1)^2 / y] dy A la izquierda por partes: u=lnx; du= dx/x; v= (1/3)x^3; dv=x^2*dx; (1/3)x^3lnx - ∫ (1/3) x^2; integro: (1/3)x^3lnx - (1/9) x^3; A la derecha: ∫ (y^2+2y+1)dy / y; o: ∫ (y + 2 +...

Consignas: dV/dt= 3 cm^3 / s; h=5 cm; r=1.5 cm (porque está a 5 cm de altura). Vol del cono de h=10 cm y r=3cm: V = (π r^2*h) / 3 dV / dt = [(π r^2) / 3 ]*(dh /dt); Derivando dt; (recordar que V es función de h, y el radio al que referimos la...

Los intereses son el 60% del capital: Capital=1 (o 100%), e intereses=0.60 (o 60%); sumados= 1.60; 5% Anual: 0.05; que sumado al capital inicial (1 o 100%) nos da: 1.05. n= Número de períodos (en este caso: número de años). 1.60 = (1.05)^n; Despejo...

(𝑦2+𝑥𝑦)𝑑𝑥−𝑥2𝑑𝑦=0; Corroboro homogeneidad: (k^2y^2 + k^2xy)dx - k^2x^2dy=0; Factorizo: k^2[ (𝑦2+𝑥𝑦)𝑑𝑥−𝑥2𝑑𝑦]=0; Es una ED Homogénea en segundo grado de homogeneidad. y=ux; dy=xdu + udx; además: u=y/x [(ux)^2 + xux]dx - x^2(xdu + udx) =...

Respuesta c) k=3. Como las raíces son inversas multiplicativas (a; 1/a), aplico Baskara: [3p + √ (9p^2 - 4k +8)] / 2 = 2 / [3p - √ (9p^2 - 4k +8)]; [3p + √ (9p^2 - 4k +8)] * [3p - √ (9p^2 - 4k +8)] = 4; a la izquierda: diferencia de cuadrados: 9p^2 -...

Entiendo que hay que integrar respecto a t, aunque no lo especificas: ∫ (6 + 4t)dt; 6t + 2t^2 + C; las unidades quedan en m/s, lo cual es correcto ya que partimos de una aceleración y al integrarla queda una velocidad. ∫ (8 - 4t)dt; 8t - 2t^2 + C;...

17. y=ln (x^2*sinx); derivación en cadena: y ' = [1 / (x^2*sinx)] * (2x*sinx + x^2cosx); o: y ' = [1 / (x^2*sinx)] * x(2*sinx + xcosx); simplifico: y ' = [1 / (x*sinx)] * (2*sinx + xcosx). 18. y= e^(3xcos√x); y ' = e^(3xcos√x) * {3cos√x - [(3xsen√x...

El costo marginal representa al "aumento del costo por producir una unidad más"; en la práctica, el costo marginal promedio es la derivada del costo respecto a la cantidad. 1). C(X) = (100+X^2)^1/2 ; dC/dx = (1/2)*(100+x^2)^(-1/2) * 2x; dC/dx = x /...

dC/dt = t^2 + 1; Para 3 s: 9+1= 10 A; Para alcanzar 20 A: 20 A = t^2+1; t(20A) = √ 19; t (20A) = 4.36 s

Según interpreto existen tres momentos analizados: 1) 0-15s; con velocidad que sube de 0 a 50 m/s, que podemos representar como una función V en relación al tiempo, con una recta: dV/dt= 50 m/s / 15 s; (10/3) m/s^2; que a su vez es nuestra...