1. Escribir la ecuación diferencial que responde a la siguiente condición y determinar su solución así como la gráfica de la sol
1. Escribir la ecuación diferencial que responde a la siguiente condición y determinar su solución así como la gráfica de la solución general correspondiente:
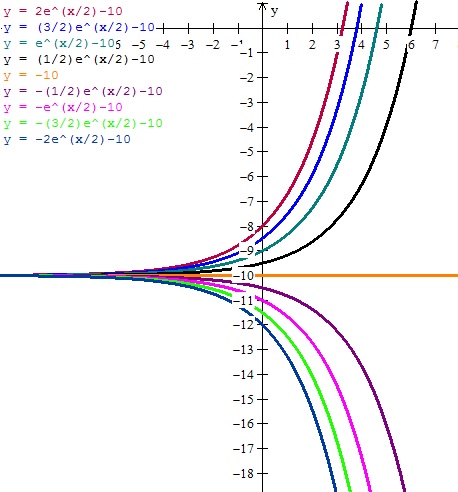
a) En cada punto (x, y) el doble de la pendiente de la tangente es igual a la ordenada del punto aumentada en 10 unidades.
b)La pendiente de una familia de curvas en cualquier punto (x, y) del plano XY está dada por 2+3x
2 Respuestas
Me podría ayudar con está ecuación
e^senx es solución de: y'+(cosx)y=0
Antonio Martinez!
a) Cuando dicen pendiente de la tangente quieren decir derivada, derivada de y respecto de x. Y la ordenada es la coordenada y de un punto. Luego la ecuación diferencial es:
2y' = y+10
2y' - y = 10
Es una ecuación diferencial con coeficientes constantes. La ecuación característica de la homogénea es
2k- 1 = 0
k = 1/2
La solución general de la homogénea es
y = C1 e^(x/2)
Y una solución particular es y=-10, se ve a simple ojo
Luego la solución general es
y=C1·e^(x/2) - 10
Esta es la gráfica:
Y eso es todo, es un ejercicio con deducción de ecuación, resolución y gráfica, ya esta bien con un ejercicio por pregunta. Si quieres el otro mándalo en otra pregunta.