Máximos, mínimos y gráfica de una función
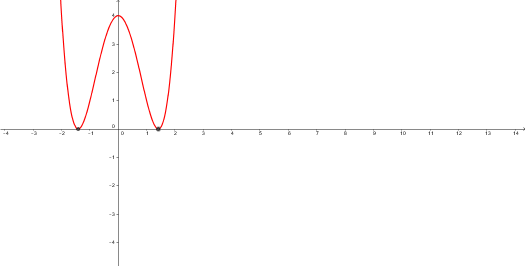
Graficar la función f(x)=x^4-4x^2
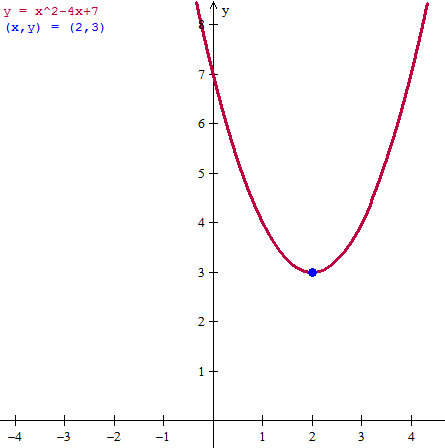
Hallar los valores máximos y/o mínimos de la función y=x^2-4x+7
Hallar los máximos y mínimos de la función f(x)=x^5-5x+6
Hallar los máximos y mínimos de la función f(x)=x^3-3x^2-9x+15
Graficar la curva f(x)=x^3-4x
Graficar la curva f(x)=x^4-4x^2+4
2 Respuestas
Respuesta de Lucas m
1
Respuesta de Valero Angel Serrano Mercadal
1