Un cierto automóvil se deprecia de acuerdo con la fórmula , como planteo este problema?
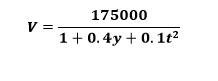
Donde t=0 representa el momento de la compra.
a) ¿A qué ritmo se deprecia el coche a un año después de la compra?
b) ¿En cuántos años el valor del coche se deprecia a la mitad de su valor?
3 Respuestas
Respuesta de Lucas m
1
Respuesta
1
Respuesta de Valero Angel Serrano Mercadal
1
