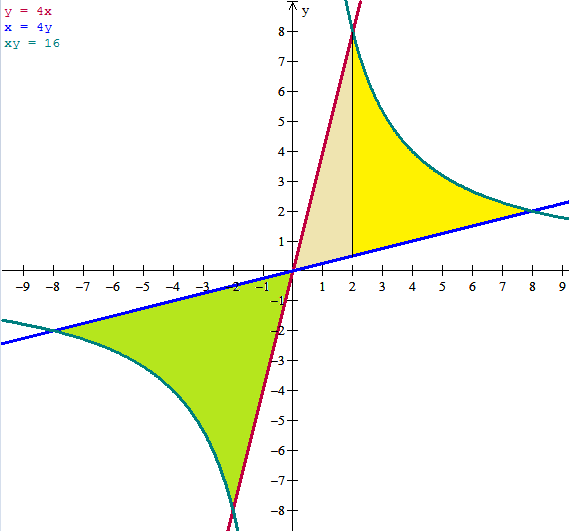·
Eso son tres ejercicios de nivel y hay que mandarlos en tres preguntas distintas. Haré el primero de ellos y si quieres los otros manda otras dos preguntas.
·
Son dos rectas pasando por el origen y otra curva que hace como la parte izquierda de la U, y uno puede imaginar la figura, pero lo mejor es hacer la gráfica para verlo.
·
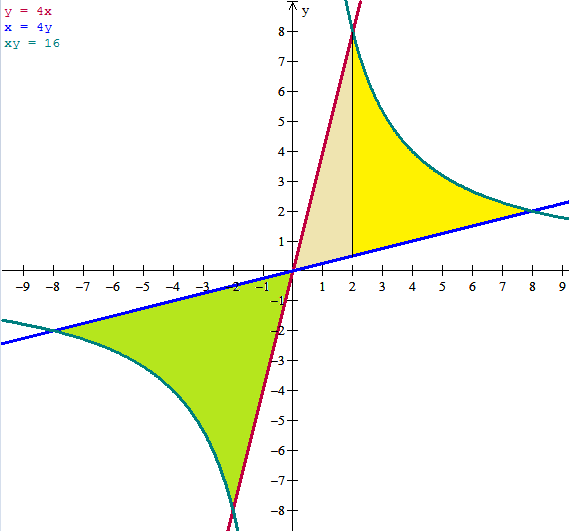
Vemos que son dos áreas con simetría en el punto (0,0). Yo no sé si querían solo un área o las dos, pero al no ser más claros son las dos. Lo que puede hacerse es calcular el área de la de arriba y se multiplica por 2. Asímismo, mirando la de arriba se ve que la función superior no siempre es la misma, luego hay que dividir tal como se ha hecho la región superior en dos partes y calcular el área de cada una y luego sumarlas.
Necesitamos los puntos de limite que en la gráfica se ve cvuáles son, pero los deduciremos analíticamente.
El límite derecho es la intersección de
y=4x
x=4y
sustituyendo la y de la primera en la segunda
x=4·4x = 16x
-15x = 0
x=0
·
El límite de la región marrón es la interseccion de
y=4x
xy=16
hacemos la misma sustitución de antes
x·4x = 16
4x^2 = 16
x^2 = 4
x = 2 y -2
la que nos interesa es x=2
·
Y el límite de la zona amarilla es la intersección
x=4y
xy=16
despejando y en la primera y=x/4 y sustituyendo en la segunda
x·x/4 = 16
x^2 = 64
x= 8 y -8 que la que nos interesa es 8
Y además tenemos que hacer todas las funciones de la forma y=f(x)
Luego la azul será
y=x/4
y la verde
y=16/x
Luego el área de la región superior es
$$\begin{align}&\int_0^2 \left(4x-\frac x4\right)dx+\int_2^8 \left(\frac {16}x-\frac x4 \right) dx=\\&\\&\int_0^2 \frac {15}4x\;dx+ \left[16 ln|x|-\frac {x^2}8 \right]_2^8=\\&\\&\frac {15}8x^2\bigg|_0^2+16(ln8-ln2)-\frac 18(64-4)\\&\\&\frac {15}2+ 16ln \frac 82-\frac {15}2= 16ln\,4 = 32 ln\, 2\\&\\&\text{Y como son dos regiones el area total es}\\&\\&A=64ln\,2\\&\\&\text{Que para hacerte una idea es}\\&\\&A= 44.36141956\end{align}$$·
Y eso es todo.