A la función y = (x) = encuentra su dominio, su rango, sus intersectos, sus simetría y su gráfica.

Esto ya es otra cosa

·

$$\begin{align}&y=f(x)=\frac{1}{\sqrt{x-1}}\end{align}$$

Para que haya dominio debe ser no negtivo lo de dentro de la raíz cuadrada

x-1>=0

x >= 1

Pero el denominador no puede ser 0

x-1=0

x=1

x deber ser distinto de 1

luego de la conjunción de ambas se tiene

Dom f = (1, infinito)

La función es positiva siempre luego el rango será positivo, veamos si cualquier número positivo perteneca al rango.

Se trata de una función continua.  El limite por la derecha en x=1 es 1/0+ = +infinito

Y el límite en +infinito es 1/infinito = 0, aunque nunca llega a valer 0

Luego por ser continua toma todos los valores entre + infinito y 0, el rango es

Rango f = (0, + infinito)

·

No tiene intersección con los ejes, no tiene con el eje Y porque el dominio empieza en x=1. Y no tiene intersección con el X porque es siempre positiva.

·

No tiene simetrias geométricas aunque pueda parecerlo.

Y esta es la gráfica.

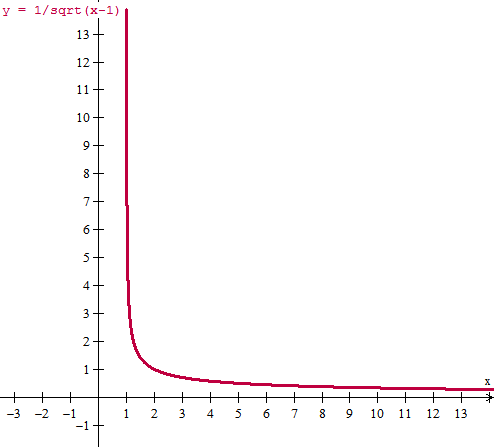
Y eso es todo.