Es de matematicas siempre seleccionare como mejor respuesta

·

Aunque parezca que hay cosas que sobran y el verbo encontrar no es el más claro yo creo que quieren que dibujes la función

F(x) = e^x

Para hacerlo sin ordenador hay que saber algunos detalles de la gráfica y unos poquitos datos para dibujarla más exacta.

De esta función podemos decir que es siempre positiva. Que en el -infinito su valor tiende a cero ya que

$$\begin{align}&\lim_{x\to -\infty}e^x= \frac{1}{e^{\infty}}=\\&\\&\text{como e > 1} \implies e^{\infty}\to\infty\\&\\&=\frac{1}{\infty}=0\end{align}$$

Y en infinito el límite es infinito como ya hemos visto, luego es una función que empieza pegada a 0 y sube hasta el infinito.  Además es siempre creciente como es lógico pensar o como se puede deducir del signo de la derivada, pero es que no estoy seguro si has dado ya las derivadas.  Por ser siempre creciente y empezar por arriba del 0 no tiene cortes con el eje X.

Tambíen si hubieras dado derivadas sabrías que la derivada segunda es e^x siempre positiva y por lo tanto es concava hacia arriba, esta siempre por debajo de un segmento entre dos de sus puntos.

Y el corte con el eje Y es

e^0 = 1

Luego pasa por el punto (0,1)

Y algunos puntos para dibujarla pueden ser

X y
-------------
-1 0.367879
-0.5 0.606531
0 1
0.5 1.648721
1 2.718282

Y para terminar dibujamos la gráfica.

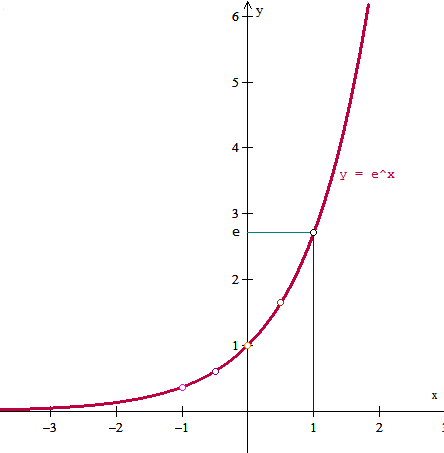
Y eso es todo.