Resolver por medio del teorema fundamental del calculo.
Sea g(x)=
$$\begin{align}&∫_0^x▒f(t)dt\end{align}$$donde f es una función cuya gráfica se muestra abajo.
a) Evalue g(0), g(1), g(2), g(3) y g(6)
b) ¿Sobre cuáles intervalos g es creciente?
c) ¿Dónde g tiene un valor máximo?
d) Dibuje una gráfica aproximada de g
1 respuesta
·
·
¡Hola Esteban!
El teorema fundamental dice que esa integral es el valor de la función primitiva en x menos el valor en 0
La función primitiva es aquella tal que al derivarla nos da la función f(x).
a) g(0) será el valor de una función (la que sea) en 0 menos el valor de ella misma en 0, luego es 0.
·
Entre 0 y 1 tenemos f(x)=2
Una primitiva de f(x) en ese intervalo es h(x)=2x
Da lo mismo poner la constante o no ya que después se cancela en la resta.
Luego g(1) = h(1)-h(0) = 2·1 - 2·0 = 2
·
Entre 1 y 2 la función es f(x)=2x, luego la primitiva es h(x)=x^2
Entonces
$$\begin{align}&g(2)=\int_0^2f(x) dx=\int_0^1f(x)dx+\int_1^2f(x)dx=\\&\\&2x\bigg|_0^1+x^2\bigg|_1^2=2-0+4-1=5\\&\\&---\\&\\&\text{Entre 0 y 3 la función es }f(x)=12-4x\\&\text{puedes comprobarlo, haz la ecuación de la recta que pasa}\\&\text{por(2,4) y (3,0)}\\&\\&h(x)=12x-2x^2\\&\\&g(3)=\int_0^3f(x)dx=\int_0^2f(x)dx+\int_2^3f(x)dx=\\&\\&g(2)+\left[12x-2x^2 \right]_2^3=5+36-18-24+8=7\\&\\&-----\\&\\&\text{Para g(6) hay que dar dos pasos, calculando primero g(5)}\\&\text{ya sabes ecuación que pasa por (3,0) y (5,-2) es}\\&f(x)=3-x\\&\\&g(5)=g(3)+\int_3^5(3-x)dx=7+\left[3x- \frac {x^2}2\right]_3^5=\\&\\&7+15-\frac {25}2-9+\frac 92=5\\&\\&\text{Entre 5 y 6 la función es }f(x)=-2\\&\\&g(6)=g(5)+\int_5^6-2dx=5-2x\bigg|_5^6(6-5)=\\&\\&5-12+10=3\end{align}$$Resumiendo las respuestas
g(0)=0, g(1)=2, g(2)=5, g(3)=7, g(6)=3
·
b) La función es creciente cuando x es positiva, luego en el intervalo [0, 3] o si se quiere ser más estricto en (0, 3)
·
c) El valor máximo es cuando pasa de ser creciente a decreciente. Luego el valor máximo es g(3)=7
·
d) Pues es dibujar todos los trozos de las primitivas, restando a cada na su valor inicial y sumándole el valor final del trozo anterior.
Te pondré las funciones sin simplificar para que veas cómo funciona el detalle ese.
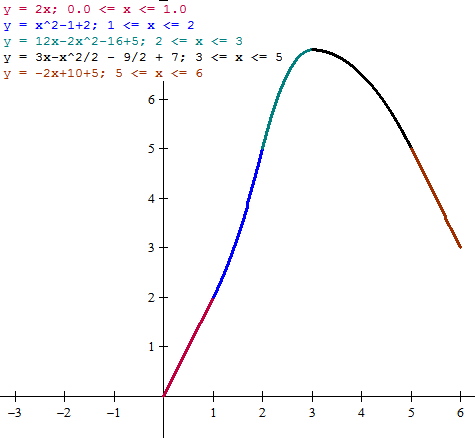
Y eso es todo, espero que te sirva y lo hayas entendido. Si no es así, pregúntame. Y si ya está bien, no olvides valorar.
Saludos.
:
:
¡Ah!
Está bien que mandes esa pregunta a Cálculo, pero mándala también a Matemáticas. Yo casi nunca miro el tema de Cálculo y veo que otros tampoco y podría quedarse allí eternamente sin contestar.
