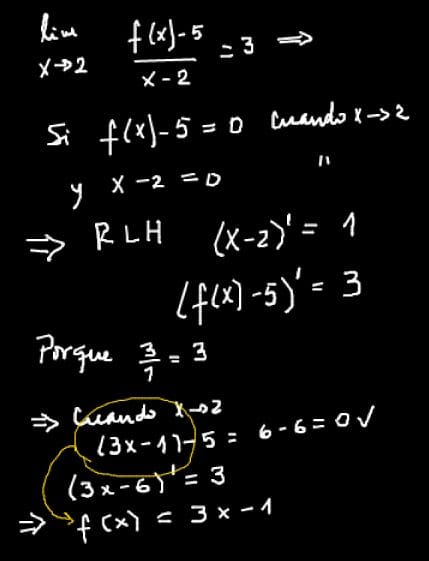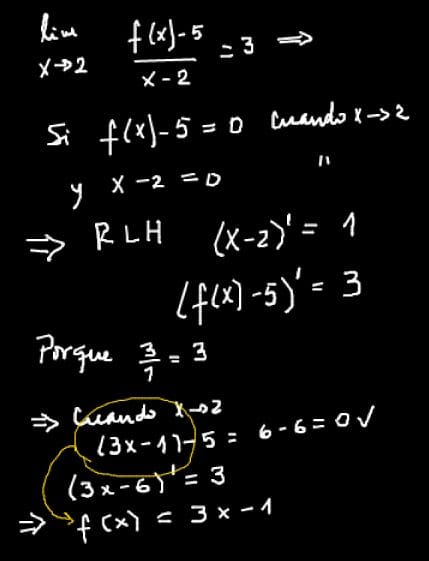Encontrar limite de una función que forma parte de otra función cuyo limite se conoce
Si lim [(f(x)-5)/(x-2)] = 3 cuando x tiende a 2, encuentra el limite de f(x) cuando x tiende a 2.
1 Respuesta
Ana Paola.
Esperaba que alguien te responda pero como no ha sido así, respondo yo con un método que no sé cómo demostrarlo.
Cuando x tiende a 2, el denominador da cero, eso da una pista.
Por la regla de L'Hopital sabemos que si una función da 0/0 , entonces su límite, si es que existe, se puede encontrar derivando numerador y denominador, luego a lo que se obtiene se reemplaza por el valor al que tiende la variable y el resultado será el límite. Ok, si derivas x - 2 el resultado es 1, entonces para que el límite de la nueva función de 3, necesariamente el numerador tendrá que ser 3.
Entonces, tenemos que encontrar una función que tenga como derivada 3 y que restada 5 dé 0.
No sé si te permiten usar la regla de L'Hopital, pero no se me ocurre otra forma de encontrar la f(x).
