Error en una serie de Taylor
a) Calcula el desarrollo en serie de Maclaurin de la función f (x) = ln(1+x).
b) Determina cuántos términos de la serie anterior son necesarios para calcular ln(1,2) con un error menor o igual que 10^(-4)
c) Se define la función g(x) como la integral de ln(1+t)/t entre los límites de integración "x" y "0". Calcula g(0,1) con un error inferior a 10^(-3).
1 Respuesta
Aquí la parte a). Sabes, yo aún no doy examen de esto y pensaba que te pedían el grado del polinomio al que había que desarrollar. Estaba esperando que alguien responda para saber cómo se resuelve, pero como no ha habido respuesta, yo he desarrollado para los cuatro primeros grados y dejo en puntos suspensivos los siguientes. Supongo que lo que cuenta es que se vea que conocemos el método de cálculo de este polinomio. Bueno aquí el desarrollo.
Ahora los siguientes...
¡Gracias!
Al parecer SAntiago no ha subido la respuesta que también yo esperaba.
Aquí la parte b, después de aclararme un poco cómo hacer la comprobación.
Para comprobar cuál es el error, en este caso que el error sea menor en una cantidad determinada, que el Ln(1.2), pues hay que saber el valor de Ln(1.2) o un valor que sea aproximado con cierta cantidad de cifras significativas. Sabiendo que el desarrollo de Taylor te da un resultado más aproxima cuando mayor sea su grado, pues yo he usado como valor "bueno", el resultado del cálculo del polinomio en grado 10. Luego calculo la derivada (n+1) del error que está acotado al valor que pide el problema. Empiezo el tanteo a grado 5 (del polinomio) y si me resulta excesivamente pequeño empiezo a bajar el grado hasta que sea cercano y menor que 0.0001 que es lo que piden.
Aquí cómo lo he hecho, espero que SAntiago o alguien más pueda confirmar que está bien
Si no está muy claro, me preguntas y lo detallo un poco más
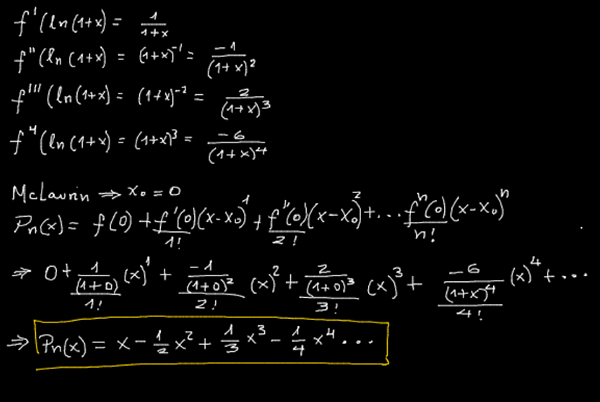
Yo estaba a cargo de la pregunta je je, pero gracias... ahora lo se tiene que hacer es hallar el grado posible que hace que la aproximación tenga un error estrictamente menor que 10^(-3) (literal c), para eso, puedes apoyarte en la fórmula del resto para calcular el error... de esa manera garantizas el grado más cercano y el literal b, es de manera análoga. Si gustan pueden intentar terminarlo... busquen la fórmula del resto para hallar el error... obtengas las derivadas necesarias... y tendrán el grado requerido. Con todo en las próximas horos lo estaré subiendo. Saludos - Santiago Seeker