Hola buenas noches, ¿Podrían ayudarme a graficar este problema?
El gasto global en viajes y turismo (en miles de mil de dólares) se describe por medio de la ecuación:
Y= 0.442x2+23.126x+181.178
Donde “x” es igual al número de años que han pasado desde 1987.
Se pide:
Encuentre el año en que se proyecta que el gasto alcance $820.5 mil millones.
Se supone que se puede graficar pues estamos en la unidad de parábolas.
1 respuesta
Dices que la función se mide en miles de mil de dolares, mientras que el gasto alcance es 820.5 mil millones. Yo creo que en la unidad de la función quisiste decir miles de millones. Si no es así ya me lo dirás.
Entonces sustituimos tal cual el valor de la función por los 820.5
0.442x^2 + 23.126x + 181.178 = 820.5
Y ahora resolvemos
0.442x^2 + 23.126x - 639.322 = 0
$$\begin{align}&x=\frac{-23.126\pm \sqrt{23.126^2+4·0.442·639.322}}{2·0.442}=\\ &\\ &\\ &\frac{-23.126\pm \sqrt{534.811876+1130.321296}}{0.884}=\\ &\\ &\\ &\frac{-23.126\pm \sqrt{1665.133172}}{0.884}=\\ &\\ &\\ &\frac{-23.126\pm 40.80604333}{0.884}=\\ &\\ &\\ &20.00004901\quad y \quad-72.32131598\\ &\end{align}$$La respuesta negativa evidentemente no sirve para nuestro problema y la que sirve es la primera que vamos a tomarla como 20 años
Y esta es la cantidad de años transcurridos desde 1987, luego el año es:
1987 + 20 = 2007
Habría que saber cuál es la gráfica que quieres hacer
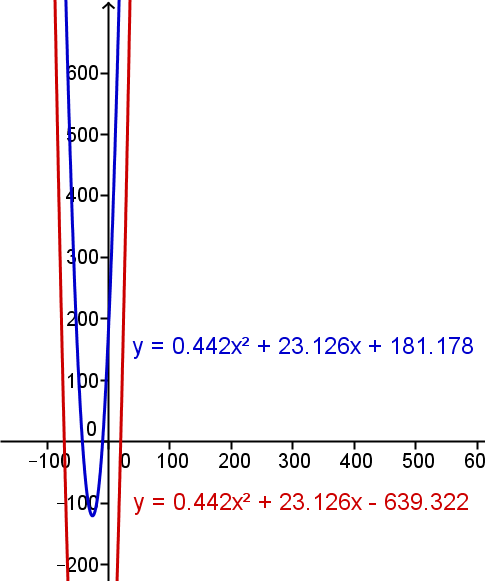
f(x) = 0.442x^2 + 23.126x + 181.178
f(x) = 0.442x^2 + 23.126x - 639.322
La primera te sirve para calcular el gasto en cualquier año. La segunda para calcular el momento exacto cuando el gasto es 820.5 miles de millones.
No sé que métodos os habrán enseñado para hacer las gráficas. Puede ser algo tan simple como hacer una tabla de valores y poner los puntos y trazar la parábola. O puede ser más completo calculando los cortes con los ejes, y el vértice de la parábola.
Es una gráfica muy empinada y no se ve nada en ella, no se pueden poner bien los años.
Y eso es todo, espero que te sirva y lo hayas entendido. Si no es así o necesitas algo más pregúntame. Y si ya está bien no olvides puntuar.
Muchas Gracias.
Tengo una duda: ¿Hasta donde llega la línea roja?
Dada una parábola en la forma
y = ax^2 + bx + c
el vértice está en el punto
x =-b/2a
luego en la parábola roja será
x = -23.126 / 0.884 = -26.16063384
y el valor de la y será
y = 0.442x^2 + 23.126x - 639.322 =
0.442(-26.16063384)^2 + 23.126(-26.16063384) - 639.322 =
302.495405 - 604.99081 - 639.322 =
-941.817405
Luego el vértice de la roja es
(-26.16063384, -941.817405)
Y el de la azul es lo mismo pero 820.5 más arriba
(-26.16063384, -121.317405)
Y eso es todo.
Ya veo, lo que pasa es que en la curva de la línea roja, sólo alcanzo a ver que rebasa los -200, en la imagen de la gráfica, esa "curva" de la línea roja hasta donde llega?
Lo que te decía, llega hasta el punto (-26.16063384, -941.817405)
Es decir hasta -941.817405 en altura y en cuanto al punto en horizontal es -26.160663384 lo mismo que el vértice de la azul. En realidad son la misma curva pero la roja está 820.5 unidades más abajo.
Y eso es todo.
me puede explicar de favor, porque el -639, pasa positivo en la fórmula?... gracias - Fab Domm
Si te refieres a la preparación de la ecuación surge de 181.178 - 820.5 = - 639.322 Si te refieres a cuando ya se soluciona mediante la fórmula ten en cuanta que la fórmula dice que dentro de la raíz cuadrada va b^2 - 4ac, por eso el conjunto -4ac queda con signo positivo ya que se multiplica menos con menos. - Valero Angel Serrano Mercadal
Una pregunta porque la ecuación de 2do grado utiliza el +4ac en positivo. Tengo entendido que es b^2 - 4ac - Jessy Vázquez