Hallar dominio, codominio, la gráfico

Veo que la han respondido completa, voy a hacer lo mismo. Preguntaba porque conozco gente que como título ponen cualquier cosa y solo quieren saber lo que se pregunta en el enunciado.

Respecto al dominio está bien claro

f(x) = 2/(x-2)   

Acuérdate que todo denominador compuesto debe ir entre paréntesis.

Y esto esté bien definido salvo en los ceros del denominador

x-2=0

x=2

Luego Dom f = R -{2}

·

El codominio es el dominio de la función inversa, para calcularla despejaremos x

y= 2/(x-2)

x-2 = 2/y

x = 2 + 2/y

Y ahora  se cambia la y por x, y la la x por f^(-1)(x)

f^(-1)(x) = 2 + 2/x

Está definida en todo R salvo en x=0 luego

Rango f = R - {0}

·

Antes de graficarla vamos a calcular algunas cosas como las asíntotas.

Tiene asíntota vertical en x=2 porque la función se hace infinito en ella.

f(x) = 2/(x-2)

Además a la izquierda de 2 tendremos x<2  ==> x-2<0 tenderá a menos infinito.

Y a la derecha x>2 ==> x-2>0  tenderá a más infinito

·

Tiene una asíntota horizontal y=0 porque el límite en ambos infinitos de la función es 0.

Veamos ahora el crecimiento y decrecimiento. Para ello calculamos la derivada

f'(x) = -1/(x-2)^2

No tiene ningún máximo o mínimo relativo porque no se hace nunca 0.

Y además es siempre decreciente porque esa derivada es negativa siempre.

Y aunque ya tenemos suficientes elementos para hacer la gráfica podemos ver la concavidad también.

La derivada segunda es

f''(x) = 2/(x-2)^3

Esto es negativo en (-infinito, 2) luego cóncava hacia abajo

Y es positivo en (2, infinito) luego cóncava hacia arriba.

Esta es la gráfica:

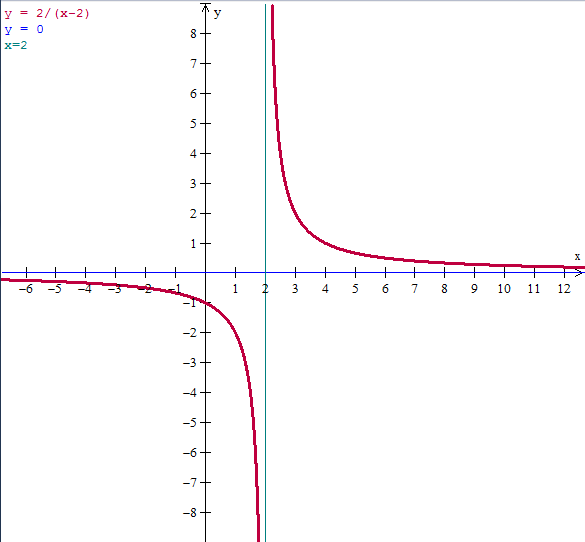
Y eso es todo.

Acostumbra a poner los parentesis. Yo voy a interpretar que la función es

f(x) = 2 / (x-2)

pero también podría ser f(x) = (2/x) - 2

Como dije, voy a resolverlo como si fuese la primera

Dom = todos los valores excepto donde se anula el denominador, luego

Dom = R - {2}

Codominio: antes de esto analicemos un poco más la función. Ya vimos que no está definida en 2, ahora veamos que pasa con la derivada, para ver los intervalos de crecimiento/decrecimiento, etc.

$$\begin{align}&f'(x) = \frac{-2}{(x-2)^2}\\&\mbox{No está definida en x=2, pero la función tampoco, así que por ese lado no hay problemas}\\&\mbox{Además vemos que el numerador es siempre negativo y el denominador siempre positivo (por ser un cuadrado)}\\&\mbox{Así que la derivada será siempre negativa y la función es estrictamente decreciente}\\&Veamos\ las\ asíntotas\\&Horizontales\ (x\to \pm\infty)\\&\lim_{x \to +\infty}\frac{2}{x-2} = 0^+\\&\lim_{x \to -\infty}\frac{2}{x-2} = 0^-\\&Verticales\ (x\to \pm 2)\\&\lim_{x \to 2^+}\frac{2}{x-2} = +\infty\\&\lim_{x \to 2^-}\frac{2}{x-2} = -\infty\\&\\&\\&\end{align}$$

Creo que ya tenemos todo lo necesario para saber que el codominio es todos los reales (pues la función tiende a +/- Infinito y es estrictamente decreciente) excepto en el cero, donde se ve que tiene una asíntota pero es fácil ver que la función nunca vale cero. Simplemente con evaluar
f(x) = 0 implica

0 = 2 / (x-2)

0 = 2 (Absurdo)

Resumiendo

Dominio = R - {2}

Codominio = R - {0}

La función es estrictamente decreciente en el dominio

Asíntotas (no las pide, pero ya que las calculamos, no está de más incluirlo)

Horizontal: y=0

Vertical: x=2

Gráfica