Indicar asíntotas de la siguiente función:

·

Un primer vistazo y ya se ve que la función va a tener asíntota(s) oblicua(s).

Pero antes vemos que no hay ninguna vertical porque la función es continua en todo x.

Y remirando vemos que hay una asíntota horizontal en -infinito y una asíntota oblicua en +infinito

El límite en -infinito es 0, el 16 no pinta nada frente a la potencia de x^2 cuando x tiende a - infinito por lo que el primer término tiende a |x|/2 y como el segundo tiende -|x|/2, el limite es 0.

Como probablemente esto no te convencerá o no te ejarán usar esa argumentación vamos a calcular el límite con las multiplicaciones y divisiones

$$\begin{align}&\lim_{x\to-\,\infty}\frac{1}{2}\sqrt{x^2+16} +\frac{1}{2}x=\\&\\&\lim_{x\to-\,\infty}\frac{\sqrt{x^2+16} +x}{2}=\\&\\&\lim_{x\to-\,\infty}\frac{\sqrt{x^2+16} +x}{2}·\frac{\sqrt{x^2+16}-x}{\sqrt{x^2+16}-x}=\\&\\&\lim_{x\to-\,\infty}\frac{x^2+16 -x^2}{2(\sqrt{x^2+16}-x)}=\\&\\&\lim_{x\to-\,\infty}\frac{16}{2(\sqrt{x^2+16}-x)}=\\&\\&\lim_{x\to-\,\infty}\frac{8}{\sqrt{x^2+16}-x}=\frac{8}{\infty+\infty}=0\\&\end{align}$$

Luego la asíntota en -infinito es horizontal y es la recta y=0

.

Y en +infinito se ve que al dividir por x va a quedar un límite finito, por eso hay una asíntota oblicua cuya pendiente es:

$$\begin{align}&m=\lim_{x\to+\infty}\frac{f(x)}{x}=\\&\\&\lim_{x\to+\infty}\frac 12· \frac{\sqrt{x^2+16}}{x}+ \frac 12 \frac xx=\\&\\&\lim_{x\to+\infty}\frac 12· \sqrt{1+\frac{16}{x^2}}+\frac 12=\frac 12+\frac 12=1\\&\\&\text{Y la constate b de la asíntota es}\\&\\&\lim_{x\to +\infty} f(x)-mx =\\&\\&\lim_{x\to+\infty}\frac 12· \sqrt{x^2+16}+ \frac 12 x-x=\\&\\&\lim_{x\to+\infty}\frac 12· \sqrt{x^2+16}- \frac 12 x=\\&\\&\lim_{x\to+\infty}\frac {\sqrt{x^2+16}-x}{2}=\\&\\&\lim_{x\to+\infty}\frac {\sqrt{x^2+16}-x}{2}·\frac{\sqrt{x^2+16}+x}{\sqrt{x^2+16}+x}=\\&\\&\lim_{x\to+\infty}\frac {x^2+16-x^2}{2(\sqrt{x^2+16}+x)}=\\&\\&\lim_{x\to+\infty}\frac {8}{\sqrt{x^2+16}+x}=\frac{8}{\infty+\infty}=0\end{align}$$

Luego en +infinito la asíntota es oblicua y es la recta y=x

·

Hagamos la gráfica para corroborarlo.

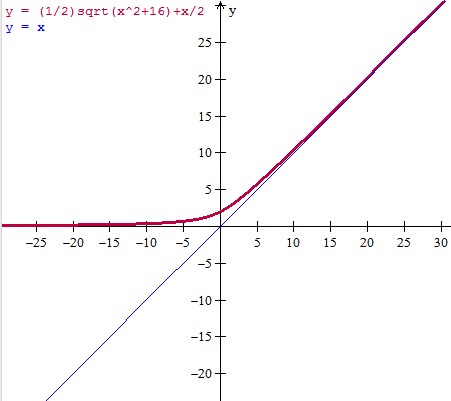
Y eso es todo.